Concretization and Abstract Post for Sign Analysis
Remember Sign Analysis for Expressions and Programs
Concrete domain  : sets of states:
: sets of states:  (three variables)
(three variables)
Abstract domain  :
: 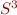
Mapping: 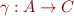 defined by:
defined by:
Constructing an Abstract Lattice
Define:
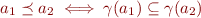
Is  a partial order?
Yes, because of the properties of
a partial order?
Yes, because of the properties of  .
.
Is it a lattice?
Abstract Postcondition
For a fixed command,
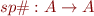
soundness condition:
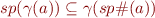
The computed set of program states will contain the most precise set of program states.
Example: Take programs with two variables. Abstract states are pairs of signs. Take statement
x = x + y
and compute its abstract strongest postcondition sp#.