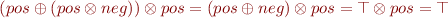Sign Analysis for Expressions and Programs

Sign Analysis for Expressions

Suppose we want to test quickly whether the result of an expression is positive, negative or zero.

What is (quickly) the sign of

$\begin{equation*} (31283321 + 8629184) \times (-34234) \times (-4 + (123123 \times (-3))) \end{equation*}$

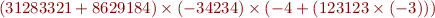
Why?

What is (quickly) the sign of

$\begin{equation*} (28166461706 + (723497 \times (- 38931))) \times 42 \end{equation*}$

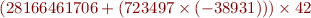
Concrete domain: 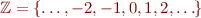$\mathbb{Z} = \{ \ldots, -2, -1, 0, 1, 2, \ldots \}$

Concrete operations: 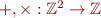${+}, {\times} : \mathbb{Z}^2 \to \mathbb{Z}$

Abstract domain: 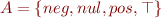$A = \{ neg, nul, pos, \top \}$

Abstract operations: 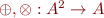$\oplus, \otimes : A^2 \to A$ defined by tables:

$\begin{tabular}{ |c |c |c |c |c |c |} \hline \oplus & neg & nul & pos & \top \\ \hline neg & neg & neg & \top & \top \\ \hline nul & neg & nul & pos & \top \\ \hline pos & \top & pos & pos & \top \\ \hline \top & \top & \top & \top & \top \\ \hline \end{tabular}$

$\begin{tabular}{ |c |c |c |c |c |c |} \hline \otimes & neg & nul & pos & \top \\ \hline neg & pos & nul & neg & \top \\ \hline nul & nul & nul & nul & nul \\ \hline pos & neg & nul & pos & \top \\ \hline \top & \top & nul & \top & \top \\ \hline \end{tabular}$

Sign Analysis for Programs

Abstract state $V \to A$ , maps each variable to element of $A$

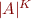We have $|A|^K$ possible states for $K$ variables.

Computation over control-flow graph for our example

a more complex 'table' than above
given
- an abstract state (sign or each var)
- a control-flow graph edge
- find state at the other end of the edge
rules for merging abstract states

When is such computation correct?

What does it even mean for such computation to be correct?