LARA – Lab for Automated Reasoning and Analysis -

Separation logic

In reference 2 below, Reynolds introduces separation logic, which is an extension of Hoare logic which permits reasoning about programs with mutable shared data structures. Assertions are extended using a separation conjuction that asserts that its subformulas hold for disjoint parts of the heap, and a closely related separating implication. Together with the definition of predicates, this extension permits the concise and flexible description of structures with controlled sharing.

The separating conjunction is a logical operation $P*Q$ that asserts that $P$ and $Q$ hold for disjoint parts of the heap. i.e. you can split the heap s.t. $P$ holds for one portion and $Q$ for the other. The precise semantics are as follows:

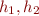$h_1, h_2$ - partial functions from locations to values. i.e. they represent a part of the heap.

$\begin{equation*} [[F_1 * F_2]]h = \exists h_1,h_2. \mbox{disjointDomains}(h_1,h_2)\ \land\ h=h_1\cup h_2\ \land\ [[F_1]]h_1\ \land\ [[F_2]]h_2 \end{equation*}$

In English: $F_1 * F_2$ is true in a heap $h$ if there exist two parts of the heap $h_1$ and $h_2$ such that all of the following are true:

$h_1$ and $h_2$ have disjoint domains
$h$ is the union of $h_1$ and $h_2$
$F_1$ is true for all locations in $h_1$
$F_2$ is true for all locations in $h_2$

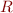In Hoare logic, you have rules like this {P}S{Q} where $P$ is the formula that must be true before the statement $S$ executes (the precondition) and $Q$ is the formula that must be true after $S$ executes (postcondition). So what we want to do here is to infer the frame rule {P*R}S{Q*R} from {P}S{Q}, so that we can make sure that no variable occurring in $R$ is modified by $S$ . This allows you to extend the specification to the variables and parts of the heap that are actually used by $S$ (this is referred to as the footprint of $S$ ). As Reynolds says, the frame rule is the key to “local reasoning” about the heap. Then he quotes another paper (reference 24 in his paper):

“To understand how a program works, it should be possible for reasoning and specification to be confined to the cells that the program actually accesses. The value of any other cell will automatically remain unchanged.”

List example

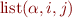To prove properties about a list, sequences are used as abstract values. In the following example, $\alpha$ and $\beta$ denote sequences, and $\epsilon$ denotes an empty sequence. To describe the representation of a singly-linked list we write $\mbox{list}(\alpha,i,j)$ where where there is a list segment from i to j representing the sequence $\alpha$ .

Inductive definitions:

$\begin{equation*} \begin{array}{rcl} \mbox{list}(\epsilon,i,j) &=& \mbox{emp} \land i=j \\ \mbox{list}(x::xs,i,k) &=& (i \mapsto x,j) * \mbox{list}(xs,j,k) \end{array} \end{equation*}$

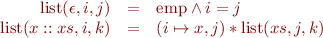
Here a list has been generalized list segments where the separating conjunction is used to prohibit cycles within the list segment.

This is about all we covered in class. On page 10 of Reynold's paper there is an example of a removal from a linked list, when I did not present here since it's easy to follow if you just consult the notations in the paper. For those who are bored by such small examples, there is also a more involved example with the body of a while loop, where the final assertion is the invariant of the while command.

References

Shape analysis with inductive recursion synthesis:

uses separation logic
infers inductively defined predicates automatically using inductive recursion synthesis (looks at code that constructs data structure)
truncation points: tree-like structures with 'holes'
interprocedural analysis
infers loop invariants and shapes for recursive procedures
program slicing reduces the size of analyzed program, based on Steesgaard-like analysis (x.f=y with x,y same type means recursive data structure)
no user-supplied annotations

Illustrates the depth and achievements of modern shape analysis research.