This is an old revision of the document!
Review of Fixpoints in Semantics
Definition: Given a set  and a function
and a function 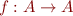 we say that
we say that  is a fixed point (fixpoint) of
is a fixed point (fixpoint) of  if
if 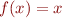 .
.
Definition: Let 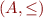 be a partial order, let
be a partial order, let 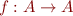 be a monotonic function on
be a monotonic function on 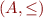 , and let the set of its fixpoints be
, and let the set of its fixpoints be 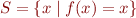 . If the least element of
. If the least element of  exists, it is called the least fixpoint, if the greatest element of
exists, it is called the least fixpoint, if the greatest element of  exists, it is called the greatest fixpoint.
exists, it is called the greatest fixpoint.
Note:
- a function can have various number of fixpoints. Take
 ,
, 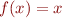 the set of fixedpoints is
the set of fixedpoints is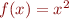 the set of fixedpoints is
the set of fixedpoints is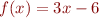 has exactly one fixpoint
has exactly one fixpoint
- a function can have at most one least and at most one greatest fixpoint
We can use fixpoints to give meaning to recursive and iterative definitions
- key to describing arbitrary long executions in programs
Transitive Closure as Least Fixedpoint
Recall the definition of transitive closure for  a binary relation
\[
a binary relation
\[
r^* = \bigcup_{n \ge 0} r^n
\]
where 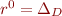 .
.
Lemma: Reflexive transitive closure is the least fixpoint of function 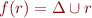 , mapping
, mapping 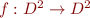
Meaning of Recursive and Iterative Constructs as Fixpoints of Relations
Consider program with single loop:
while (c) {
s;
}
Using tail recursion, we could rewrite it as a procedure p such that
p = if (c) then (s;p) else skip
This can be written as \[
p = F(p)
\] where
F(p) = if (c) then (s;p) else skip
How to give semantics to recursive definitions?
- eliminate recursive by denoting left-hand side as the result of non-recursive function

- look for solution of
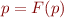 , which contains
, which contains  twice, so it expresses recursion
twice, so it expresses recursion - we can abstract the question of existence of values of recursive functions using fixpoints
If  is meaning of
is meaning of  and
and  is meaning of assume( c ), the meaning is the fixpoint of function
\[
is meaning of assume( c ), the meaning is the fixpoint of function
\[
f(r) = (\Delta_c \circ r_s \circ r) \cup \Delta_{\lnot c}
\]
Any program can be reduced to a loop:
- introduce program counter and iterate until it reaches exit point
- more generally, can write an interpreter that interprets the program
Recall Relational semantics of procedures.
What is the fixpoint of the recursive function 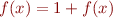 mapping integers to integers?
mapping integers to integers?
- we need ordering to ensure existence of fixpoints
- relations have a natural subset ordering
- relation does not always represent terminating computation
Reachable States and Collecting Semantics
Main question: What values can variables of the program take at different program points?
We can represent programs by control-flow graphs (CFG).
Definition: Control flow-graph is a graph with nodes  , edges
, edges 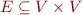 and for each edge
and for each edge  a command
a command 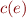 , with initial
, with initial  and final node
and final node 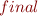
Program points are CFG nodes. Statements are labels on CFG edges.
We look at a particular way of representing and computing sets of reachable, splitting states by program counter (control-flow graph node): collecting semantics.
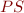 - the set of values of program variables (not including program counter).
- the set of values of program variables (not including program counter).
For each program point  , we have the set of reachable states
, we have the set of reachable states 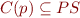 .
.
The set of all reachable states of the program is 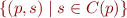 .
.
Let  be initial program counter and
be initial program counter and  the set of values of program variables in
the set of values of program variables in  .
.
The set of reachable states is defined as the least solution of: