This is an old revision of the document!
Review of Fixpoints in Semantics
Definition: Given a set  and a function
and a function 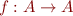 we say that
we say that  is a fixed point (fixpoint) of
is a fixed point (fixpoint) of  if
if 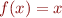 .
.
Definition: Let 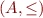 be a partial order, let
be a partial order, let 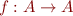 be a monotonic function on
be a monotonic function on 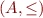 , and let the set of its fixpoints be
, and let the set of its fixpoints be 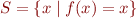 . If the least element of
. If the least element of  exists, it is called the least fixpoint, if the greatest element of
exists, it is called the least fixpoint, if the greatest element of  exists, it is called the greatest fixpoint.
exists, it is called the greatest fixpoint.
Note:
- a function can have various number of fixpoints. Take
 ,
, 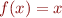 the set of fixedpoints is
the set of fixedpoints is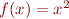 the set of fixedpoints is
the set of fixedpoints is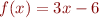 has exactly one fixpoint
has exactly one fixpoint
- a function can have at most one least and at most one greatest fixpoint
We can use fixpoints to give meaning to recursive and iterative definitions
- key to describing arbitrary long executions in programs
Transitive Closure as Least Fixedpoint
Recall the definition of transitive closure for  a binary relation
\[
a binary relation
\[
r^* = \bigcup_{n \ge 0} r^n
\]
where 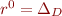 .
.
Lemma: Reflexive transitive closure is the least fixpoint of function 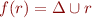 , mapping
, mapping 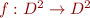
Relations and Reachable States Fixpoints
Consider program with single loop:
while (c) {
s;
}
Using tail recursion, we could rewrite it as procedure p such that
p = if (c) then (s;p) else skip
This can be written as \[
p = F(p)
\] where
F(p) = if (c) then (s;p) else skip
If  is meaning of
is meaning of  and
and  is meaning of assume©, the meaning is the fixpoint of function
\[
is meaning of assume©, the meaning is the fixpoint of function
\[
f(r) = (\Delta_c \circ r_s \circ r) \cup \Delta_{\lnot c}
\]
Any program can be reduced to a loop:
- introduce program counter and iterate until it reaches exit point
- more generally, can write an interpreter that interprets the program
Collecting Semantics
Particular way of representing and computing sets of reachable, splitting states by program counter.