Remarks on WS1S Complexity

Complexity of One Algorithm

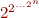The construction in Using Automata to Decide WS1S determinizes automaton whenever it needs to perform negation. Moreover, existential quantifier forces the automaton to be non-deterministic. Therefore, with every alternation between $\exists$ and $\forall$ we obtain an exponential blowup. For formula with n alternations we have $2^{2^{\ldots 2^{n}}}$ complexity with a stack of exponentials of height $n$ . Is there a better algorithm?

Reference

A. R. Meyer: Weak monadic second order theory of successor is not elementary recursive, Preliminary Report, 1973.

Lower Bound

The following paper shows that, in the worst case such behavior cannot be avoided, because of such high expressive power of MSOL over strings.

Cosmological Lower Bound on the Circuit Complexity of a Small Problem in Logic (See the introduction and the conclusion sections)