This is an old revision of the document!

Polynomial Algorithm for Horn Clauses

A Horn clause is a clause that has at most one positive literal.

Such clause is either of the form 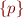$\{p\}$ where $p \in V$ is a variable, or of the form $\{\lnot p_1, \ldots, \lnot p_n, q$ for $n \ge 1$ , that is $p_1 \land \ldots \land p_n \rightarrow q$ .

The following algorithm eliminates clauses of the form 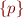$\{p\}$ , keeping only clauses that have at least one assumption.

To check satisfiability of a set of Horn clauses:

while the set contains a clause of the form 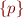$\{p\}$ where $p$ is a propositional variable:
- erase all clauses that contain literal $p$
- remove $\lnot p$ from all literals
- if there is an empty clause, set is not satisfiable
if no contradiction found, the set is satisfiable

On 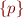$\{p\}$ we conclude that $p$ must be true and derive valid consequences of this fact. If we obtain contradiction, the set of clearly unsatisfiable.

Moreover, if loop terminates then every clause contains a negative literal. The assignment that sets all remaining variables to false is a satisfying assignment.