Boolean Constraint Propagation and Polynomial Algorithm for Horn Clauses
A Horn clause is a clause that has at most one positive literal.
Such clause is either of the form 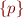 where
where  is a variable, or
is a variable, or 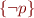 for
for  , or of the form
, or of the form 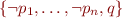 for
for  , that is
, that is  .
.
The following algorithm eliminates clauses of the form 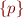 , keeping only clauses that have at least one negative literal.
, keeping only clauses that have at least one negative literal.
To check satisfiability of a set of Horn clauses:
- while the set contains a clause of the form
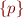 where
where  is a propositional variable, do boolean constraint propagation:
is a propositional variable, do boolean constraint propagation:- erase all clauses that contain literal

- remove
 from all clauses
from all clauses - if there is an empty clause, the set is unsatisfiable
- if no empty clause found after repeating the above, the set is satisfiable
Boolean constraint propagation is a sound inference rule. If we obtain contradiction, the set is therefore unsatisfiable.
If loop terminates and there are no empty clauses, then every clause contains a negative literal. The assignment that sets all remaining variables to false is a satisfying assignment.
This algorithm does polynomial amount of work for each propositional variable, so it is polynomial.
Conclusion: the difficulty are clauses with at least two positive literals, they require case analysis.