Notes on Congruences
We say that a relation  is a congruence with respect to a set of functions and relations iff, when we consider a first-order language containing symbols for these functions and relations and interpret 'eq' as
is a congruence with respect to a set of functions and relations iff, when we consider a first-order language containing symbols for these functions and relations and interpret 'eq' as  , the Axioms for Equality hold in the resulting structure
, the Axioms for Equality hold in the resulting structure  .
.
We next fix  as well as functions and relations and consider the set of all congruences on the set
as well as functions and relations and consider the set of all congruences on the set  with respect to these functions and relations.
with respect to these functions and relations.
We assume no relation symbols other than congruence itself. (We represent a predicate 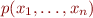 as
as 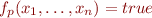 .)
.)
Intersection of Congruences
Theorem: Let  be a set of congruences. Then
be a set of congruences. Then 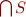 is also a congruence. Note: we define
is also a congruence. Note: we define 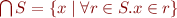 .
.
Proof:
We will consider the case of 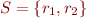 .
It case be generalized to arbitrary number of relation, because
.
It case be generalized to arbitrary number of relation, because  is associative.
is associative.
Reflexive:
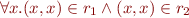 because
because 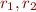 are congruence.
It implies that
are congruence.
It implies that 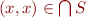 .
.
Symmetric:
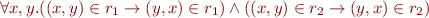 because
because 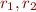 are congruence.
It implies that
are congruence.
It implies that  .
.
Transitive:
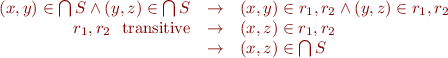
Congruence conditions:
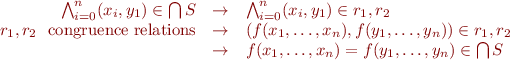
End of Proof.
Existence of the Least Congruence Containing Given Relation
Theorem: Let 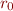 be a relation. Let
be a relation. Let  be the set of all congruences
be the set of all congruences  such that
such that  and let
and let 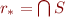 . Then
. Then  is the least congruence containing
is the least congruence containing 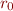 , that is
, that is
 is a congruence
is a congruence
- if
 is a congruence such that
is a congruence such that  , then
, then 
Construction of the Least Congruence Containing Given Relation
Define
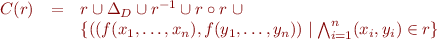
Let 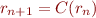 for
for  .
.
Theorem:  is the least congruence containing
is the least congruence containing 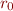 .
.
Proof (sketch):
 :
:  is a congruence that contains
is a congruence that contains 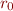 , thus
, thus  .
.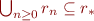 : by induction on
: by induction on  .
. :
:  by definition of
by definition of 
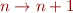 : all elements introduced by
: all elements introduced by 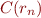 are required to be in
are required to be in  by definition of congruence, so if
by definition of congruence, so if  then also
then also 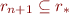
End of Proof.