Mapping Fixpoints Under Lattice Morphisms
Definition: Let 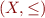 and
and 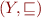 be complete lattices. We call
be complete lattices. We call 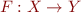 a complete join-morphism iff for each set
a complete join-morphism iff for each set  we have
we have
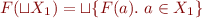
For example, 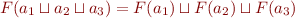 .
.
Lemma: Let 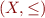 and
and 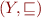 be complete lattices, and
be complete lattices, and 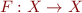 ,
, 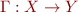 ,
,  be complete join-morphisms such that
be complete join-morphisms such that
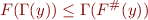
for all  . If
. If 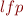 denotes least fixpoint of a function, then
denotes least fixpoint of a function, then
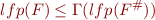
In other words, we can approximate 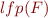 by computing
by computing 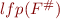 .
.