LARA

Introductory Remarks on SMT Provers

We next study techniques that help understand how modern SMT (satisfiability modulo-theories) provers work.

Meaning of name (recent):

  • satisfiability: check satisfiability of formulas (to check validity, check satisfiability of negation)
  • modulo theories: built-in support for arithmetic, arrays, algebraic data types

Example provers:

SMT Prover Architecture

Layers:

  • fast solving of quantifier-free formulas (see DPLL(T) paper)
    • SAT solver to 'enumerate' conjunctions of disjunctive normal form (Lecture 08a)
    • specialized algorithms for quantifier-free formulas - this is what we will talk about today
  • heuristic quantifier instantiation (instantiation rule)

Note: formulas that are valid in the combination of quantifiers, linear integers, and uninterpreted functions are not enumerable (and neither are formulas that are not valid). The situation is worse than in pure first-order logic.

Example

Consider the following formula, where $f$ denotes functions from integers to integers and 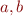$a,b$ are integers.

\begin{equation*}\begin{array}{l} (\forall x.\forall y.\ x \le y \rightarrow f(x) \le f(y))\ \land \\ (\forall x.\forall y. f(x)=f(y) \rightarrow x=y)\ \land\\ 2 f(a) \le 2f(b)+1\ \land\\ b < a \end{array} \end{equation*}

Is this formula satisfiable?

  • over integers
  • over reals