This is an old revision of the document!

Interpolation for Propositional Logic

Given two propositional formulas $F$ and $G$ , an interpolant is a propositional formula $H$ such that:
1) $\models F \rightarrow H$
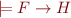
2) $\models H \rightarrow G$
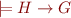
3) $FV(H)\subseteq FV(F) \cap FV(G)$

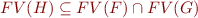
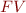$FV$ denotes the set of free variables in the given propositional formula (see Propositional Logic Syntax).

Note that $F \rightarrow G$ by transitivity of $\rightarrow$ . The interpolant extracts what makes $F$ imply $G$ .

Here are two easy ways to create an interpolant.

We can quantify existentially all variables in $F$ that are not in $G$ . We obtain the weakest interpolant:

$H_{min} \equiv \exists p_1, p_2, ..., p_n.\ F$ where $\{p_1, p_2, ..., p_n \}\ = FV(F)\backslash FV(G)$

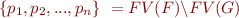
We can quantify universally all variables in $G$ that are not in $F$ . We obtain the strongest interpolant:

$H_{max} \equiv \forall p_1, p_2, ..., p_n.\ G$ where $\{p_1, p_2, ..., p_n \}\ = FV(G)\backslash FV(F)$

We can also derive interpolants from resolution proofs, as we will see in lecture07.