Homework 10, Due May 7th
Problem 1
Let  be the set of all first-order formulas (viewed as syntax trees) and let
be the set of all first-order formulas (viewed as syntax trees) and let  be the implication relation on formulas:
be the implication relation on formulas:
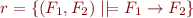
Check whether  is reflexive, antisymmetric, and transitive relation.
is reflexive, antisymmetric, and transitive relation.
Problem 2
Let 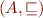 be a partial order such that every set
be a partial order such that every set  has the greatest lower bound. Prove that then every set
has the greatest lower bound. Prove that then every set  has the least upper bound.
has the least upper bound.
Problem 3
Let ![Math $A = [0,1] = \{ x \in \mathbb{R} \mid 0 \le x \le 1 \}$](/w/lib/exe/fetch.php?media=wiki:latex:/imgca97f4c49c280d1bb702717b9af0028f.png) be the interval of real numbers. Recall that, by definition of real numbers and complete lattice,
be the interval of real numbers. Recall that, by definition of real numbers and complete lattice, 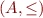 is a complete lattice with least lattice element
is a complete lattice with least lattice element  and greatest lattice element
and greatest lattice element  . Here
. Here  is the least upper bound operator on sets of real numbers, also called supremum and denoted sup in real analysis.
is the least upper bound operator on sets of real numbers, also called supremum and denoted sup in real analysis.
Let function 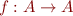 be given by
be given by
![Equation \begin{equation*}
f(x) = \left\{\begin{array}{l}
\frac{1}{2} + \frac{1}{4}x, \mbox{ if } x \in [0,\frac{2}{3}) \\
\ \\
\frac{3}{5} + \frac{1}{5}x, \mbox{ if } x \in [\frac{2}{3},1]
\end{array}\right.
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgd83cc2c72aaddd58fcdebcda8586e172.png)
(It may help you to try to draw  .)
.)
Part a)
Prove that  is monotonic and injective (so it is strictly monotonic).
is monotonic and injective (so it is strictly monotonic).
Part b)
Compute the set of fixpoints of  .
.
Part c)
Define  . (This is in fact equal to
. (This is in fact equal to  when
when  is a monotonic bounded function.)
is a monotonic bounded function.)
Compute 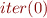 (prove that the computed value is correct by definition of
(prove that the computed value is correct by definition of  , that is, that the value is indeed
, that is, that the value is indeed  of the set of values). Is
of the set of values). Is 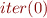 a fixpoint of
a fixpoint of  ? Is
? Is 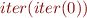 a fixpoint of
a fixpoint of  ? Is
? Is  an
an  -continuous function?
-continuous function?
Optional part d)
Define a monotonic function 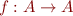 such that, for every natural number
such that, for every natural number  , the value
, the value 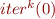 is not a fixpoint of
is not a fixpoint of  . (It may be difficult to draw
. (It may be difficult to draw  .)
.)