LARA

This is an old revision of the document!

Herbrand Universe for Equality

Recall example of formula $F$: \[ 

  P(a) \land (\forall x.\ P(x) \rightarrow \lnot P(f(x))) \land (\forall x. x=a \lor x=b)

\] Replace '=' with 'eq': \[ 

  P(a) \land (\forall x.\ P(x) \rightarrow \lnot P(f(x))) \land (\forall x. eq(x,a) \lor eq(x,b))

\] call the resulting formula $F'$.

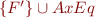Consider Herbrand model $I_H$ for $\{F'\} \cup AxEq$. The relation $e_F(I_H)(eq)$ splits $GT$ into two sets: the set of terms eq with $a$, and the set of terms eq with $b$.

Constructing Model for Formulas with Equality

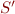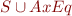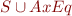Let $S$ be a set of formulas in first-order logic with equality and $S'$ result of replacing '=' with 'eq' in $S$. Suppose that $S \cup AxEq$ is satisfiable. Let $(GT,I_H)$ be Herbrand model for $S \cup AxEq$. We construct a new model using quotient construction, described as follows.

For each element $t \in GT$, define \[ 

  [t] = \{ s \mid (s,t) \in e_F(I_H)(eq) \}

\] Let \[ 

  [GT] = \{ [t] \mid t \in GT \}

\] The constructed model will be $([GT],I_Q)$ where $I_Q$ is such that \[ 

  I_Q(f)([t_1],\ldots,[t_n]) = [f(t_1,\ldots,t_n)]

\] \[ 

  I_Q(R) = \{ ([t_1],\ldots,[t_n]) \mid (t_1,\ldots,t_n) \in I_H(R) \}

\] The interpretation of eq in $([GT],I_Q)$ becomes equality.

Inductive lemma.

Herbrand-Like Theorem for Equality

Theorem: For every set of formulas with equality $S$ the following are equivalent

  • $S$ has a model
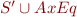  • $S' \cup AxEq$ has a model (where 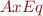$AxEq$ are Axioms for Equality and $S'$ is result of replacing '=' with 'eq' in $S$)
  • $S$ has a model whose domain is the quotient $[GT]$ of ground terms under some congruence