This is an old revision of the document!
Ground Terms as Domain of Interpretation
Recall syntax of first-order logic terms in First-Order Logic Syntax.
Ground term is a term  without variables, i.e.
without variables, i.e. 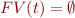 , i.e. given by grammar:
\[
, i.e. given by grammar:
\[
GT ::= f(GT,\ldots,GT)
\] i.e. built from constants using function symbols.
Example
If  has no constants then
has no constants then  is empty. In that case, we add a fresh constant
is empty. In that case, we add a fresh constant  into the language and consider
into the language and consider 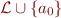 that has a non-empty
that has a non-empty  . We call the set
. We call the set  Herbrand Universe.
Herbrand Universe.
Goal: show that if a formula without equality (for now) has a model, then it has a model whose domain is Herbrand universe, that is, a model of the form  .
.
How to define 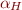 ?
?
Term Algebra Interpretation for Function Symbols
Let 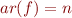 . Then
. Then 
This defines 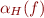 . How to define
. How to define 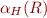 to ensure that elements of a set are true, i.e. that
to ensure that elements of a set are true, i.e. that  ?
?
- is this possible for arbitrary set?
Example
Ground Atoms
If 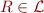 ,
, 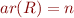 and
and 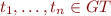 , we call
, we call 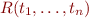 an Herbrand Atom. HA is the set of all Herbrand atoms:
\[
an Herbrand Atom. HA is the set of all Herbrand atoms:
\[
HA = \{ R(t_1,\ldots,t_n) \mid R \in {\cal L}\ \land \ t_1,\ldots,t_n \in GT \}
\]
We order elements of  in sequence (e.g. sorted by length) and establish a bijection
in sequence (e.g. sorted by length) and establish a bijection  with propositional variables
\[
with propositional variables
\[
p : HA \to V
\]
We will write 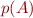 .
.
Example