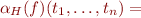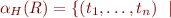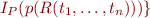This is an old revision of the document!
Ground Terms as Domain of Interpretation
Recall syntax of first-order logic terms in First-Order Logic Syntax.
Ground term is a term  without variables, i.e.
without variables, i.e. 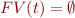 , i.e. given by grammar:
\[
, i.e. given by grammar:
\[
GT ::= f(GT,\ldots,GT)
\] i.e. built from constants using function symbols.
Example
If  has no constants then
has no constants then  is empty. In that case, we add a fresh constant
is empty. In that case, we add a fresh constant  into the language and consider
into the language and consider 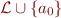 that has a non-empty
that has a non-empty  . We call the set
. We call the set  Herbrand Universe.
Herbrand Universe.
Goal: show that if a formula without equality (for now) has a model, then it has a model whose domain is Herbrand universe, that is, a model of the form  .
.
How to define 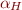 ?
?
Term Algebra Interpretation for Function Symbols
Let 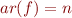 . Then
. Then 
This defines 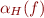 . How to define
. How to define 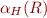 to ensure that elements of a set are true, i.e. that
to ensure that elements of a set are true, i.e. that  ?
?
- is this possible for arbitrary set?
Example
Ground Atoms
If 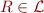 ,
, 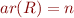 and
and 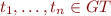 , we call
, we call 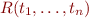 an Herbrand Atom. HA is the set of all Herbrand atoms:
\[
an Herbrand Atom. HA is the set of all Herbrand atoms:
\[
HA = \{ R(t_1,\ldots,t_n) \mid R \in {\cal L}\ \land \ t_1,\ldots,t_n \in GT \}
\]
We order elements of  in sequence (e.g. sorted by length) and establish a bijection
in sequence (e.g. sorted by length) and establish a bijection  with propositional variables
\[
with propositional variables
\[
p : HA \to V
\]
We will write 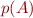 .
.
Example
Expansion of a Clause
Recall that we do not write quantifiers in the clause, but when we say that a clause is true in a model we mean that its universal closure is true.
We obtain an instance of a clause  by replacing all variables with some ground terms from
by replacing all variables with some ground terms from  .
.
Define \[
expand(C) = \{ subst(\{x_1 \mapsto t_1,\ldots,x_n \mapsto t_n\})(C) \mid FV(C) = \{x_1,\ldots,x_n\}\ \land\ t_1,\ldots,t_n \in GT \}
\]
Note that if  is true in
is true in  , then
, then 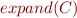 is also true in
is also true in  (
(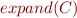 is a consequence of
is a consequence of  ).
).
We expand entire set: \[
expand(S) = \bigcup_{C \in S} expand(C)
\]
Clauses in the expansion have no variables, they are ground clauses.
Constructing a Propositional Model
We can view the set 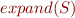 as a set of propositional variables with “long names”.
as a set of propositional variables with “long names”.
For an expansion of clause  we can construct the corresponding propositional formula
we can construct the corresponding propositional formula  .
.
Example
Define propositional model  by
\[
by
\[
I_P(p(C_G)) = e_F(C_G)(I)
\]
Let \[
propExpand(S) = \{ p(C_G) \mid C_G \in expand(S) \}
\]
Lemma: If  is a model of
is a model of  , then
, then 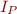 is a model of
is a model of 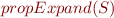 .
.
Instead of searching for a model, we can search for a propositional model.
If we prove there is no propositional model for 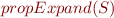 , then there is no model for
, then there is no model for  .
.
What if there is a model 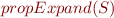 ? Could it still be the case that
? Could it still be the case that  is unsatisfiable?
is unsatisfiable?
Constructing Herbrand Model
For  we define
we define 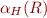 so that
so that  evaluates ground formulas
evaluates ground formulas 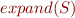 same as in
same as in 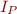 (and thus same as in
(and thus same as in  ).
).
We ensure that atomic formulas evaluate the same:
How does it evaluate non-ground formulas?
Lemma: If 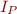 is a model for
is a model for 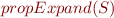 , then
, then  is a model for
is a model for  .
.
Herbrand's Theorem
Theorem: The following statements are equivalent:
- set
 has a model
has a model - set
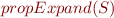 has a propositional model
has a propositional model - set
 has a model with domain
has a model with domain