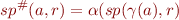Galois Connection
Galois connection is defined by two monotonic functions  and
and 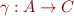 between partial orders
between partial orders  on
on  and
and  on
on  , such that
, such that

for all  and
and  (intuitively, the condition means that
(intuitively, the condition means that  is approximated by
is approximated by  ).
).
Lemma: The condition  holds iff the conjunction of these two conditions:
holds iff the conjunction of these two conditions:
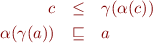
holds for all  and
and  .
.
Lemma: Let  and
and  satisfy the condition of Galois connection. Then the following three conditions are equivalent:
satisfy the condition of Galois connection. Then the following three conditions are equivalent:
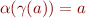 for all
for all 
 is a surjective function
is a surjective function is an injective function
is an injective function
Using Galois Connection
Terminology:
 - concrete domain
- concrete domain - abstract domain
- abstract domain - concretization function
- concretization function - abstraction function
- abstraction function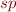 - (the usual) strongest postcondition (or just “strongest post”), also called
- (the usual) strongest postcondition (or just “strongest post”), also called - abstract post, abstract transformer (transforms one abstract element into another)
- abstract post, abstract transformer (transforms one abstract element into another)
Abstraction function for sign analysis.
Define  using
using  and
and  :
:
Best Abstract Transformer
 can in general be arbitrarily precise while preserving correctness.
can in general be arbitrarily precise while preserving correctness.
Given  , we would like
, we would like  to be as precise as possible while being correct.
to be as precise as possible while being correct.
The most precise  is called “best abstract transformer”.
is called “best abstract transformer”.
If 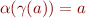 , then
, then  defined using
defined using  and
and  is the most precise one (given the abstract domain and particular blocks in the control-flow graph).
is the most precise one (given the abstract domain and particular blocks in the control-flow graph).