Forward VCG: Using Strongest Postcondition
If 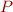 is a formula on state and
is a formula on state and  a command, let
a command, let 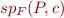 the formula version of strongest postcondition operator.
the formula version of strongest postcondition operator. 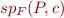 is therefore formula
is therefore formula  that describes the set of states that can result from executing
that describes the set of states that can result from executing  in a state satisfying
in a state satisfying 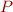 .
.
Thus, we have
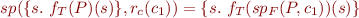
or, less formally,
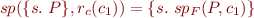
For a predicate 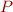 , let
, let  be the set of states that satisfies it,
be the set of states that satisfies it,
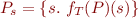
Rules for Computing Strongest Postcondition
Assume Statement
Define:
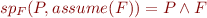
Then
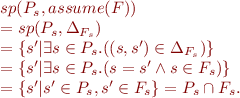
Havoc Statement
Define:
![Equation \begin{equation*}
sp_F(P,\mbox{havoc}(x)) = \exists x_0. P[x:=x_0]
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img89657fc036860a71f54d2d43719de21d.png)
Assignment Statement
Define:
![Equation \begin{equation*}
sp_F(P, x = e) = \exists x_0.(P[x:=x_0] \land x=e[x:=x_0])
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img7bc83c0c2e4ce88bae966a29224fc603.png)
Indeed:
![Equation \begin{equation*}
\begin{array}{l}
sp(P_s, r_c(x = e)) \\
= \{s'| \exists s.(s \in P_s \wedge (s, s') \in r_c(x=e))\} \\
= \{s'| \exists s.(s \in P_s \wedge s' = s[x \rightarrow f_T(e)(s)]) \}
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img97c519c28e30bd4bef7ff75f1371ac4b.png)
Sequential Composition
For relations we proved
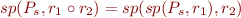
Therefore, define
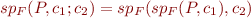
Nondeterministic Choice (Branches)
We had 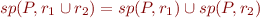 . Therefore define:
. Therefore define:
![Equation \begin{equation*}
sp_F(P,c_1 [] c_2) = sp_F(P,c_1) \lor sp_F(P,c_2)
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img2e65ec236f0d53fd347c99c2e3675b01.png)
Correctness
We show by induction on  that for all
that for all 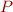 :
:
Examples
Example 1.
Precondition: 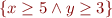 . Code:
. Code:
x = x + y + 10
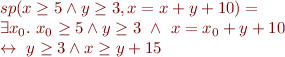
Example 2. Precondition:  . Code:
. Code:
havoc(x)
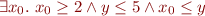
i.e.
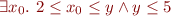
i.e.
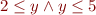
If we simply removed conjuncts containing  , we would get just
, we would get just  .
.
Size of Generated Formulas
The size of the formula can be exponential because each time we have a nondeterministic choice, we double formula size:
![Equation \begin{equation*}
\begin{array}{l}
sp_F(P, (c_1 [] c_2);(c_3 [] c_4)) = \\
sp_F(sp_F(P,c_1 [] c_2), c_3 [] c_4) = \\
sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_3 [] c_4) = \\
sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_3) \vee
sp_F(sp_F(P,c_1) \vee sp_F(P,c_2), c_4)
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img4ccaa9aeb384597a5b7f2eecc97acafb.png)
Reducing sp to Relation Composition
The following identity holds for relations (see Sets and Relations):
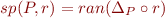
Based on this, we can compute 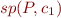 in two steps:
in two steps:
- compute formula
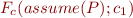 , using Compositional VCG
, using Compositional VCG - existentially quantify over initial (non-primed) variables
Indeed, if  is a formula denoting relation
is a formula denoting relation  , that is,
, that is,
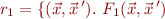
then  is formula denoting the range of
is formula denoting the range of  :
:
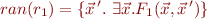
Moreover, the resulting approach does not have exponentially large formulas.