This is an old revision of the document!
First-Order Logic Syntax
(Compare to Propositional Logic Syntax.)
First order language  is a set of relation symbols
is a set of relation symbols  and function symbols
and function symbols  , each of which comes with arity
, each of which comes with arity 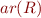 ,
,  , which are
, which are  . Function symbols of arity 0 are constants. Relation symbols of arity 0 are propositional variables.
. Function symbols of arity 0 are constants. Relation symbols of arity 0 are propositional variables.
The set  denotes countably infinite set of first-order variables, which is independent of the language.
denotes countably infinite set of first-order variables, which is independent of the language.
\[ \begin{array}{rcl}
F &::=& A \mid \lnot F \mid (F \land F) \mid (F \lor F) \mid (F \rightarrow F) \mid (F \leftrightarrow F) \\
& \mid & \forall x.F \mid \exists x.F \\
A & ::= & R(T,\ldots,T) \mid (T = T) \\
T & ::= & V \mid f(T,\ldots,T)
\end{array} \]
Terminology summary:
 - first-order logic formula (in language
- first-order logic formula (in language  )
) - atomic formula
- atomic formula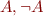 - literals
- literals - term
- term - function symbol
- function symbol - relation symbol
- relation symbol - first-order variables
- first-order variables
Omitting parentheses:
 ,
,  are associative
are associative- priorities, from strongest-binding:
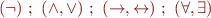
When in doubt, use parentheses.
Example: Consider language 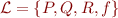 with
with 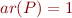 ,
, 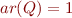 ,
, 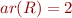 ,
, 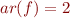 . Then
\[
. Then
\[
\lnot \forall x.\, \forall y. R(x,y) \land Q(x) \rightarrow Q(f(y,x)) \lor P(x)
\] denotes \[
\lnot (\forall x.\ (\forall y. ((R(x,y) \land Q(x)) \rightarrow (Q(f(y,x)) \lor P(x)))))
\]
Often we use infix notation for relation and function symbols. In the example above, if we write  and
and  in infix notation, the formula becomes
\[
in infix notation, the formula becomes
\[
\lnot \forall x.\, \forall y. x \mathop{R} y \land Q(x) \rightarrow Q(y \mathop{f} x) \lor P(x)
\]
Notation: when we write  this means that
this means that  and
and  are identical formulas (with identical syntax trees). For example,
are identical formulas (with identical syntax trees). For example,  , but it is not the case that
, but it is not the case that  .
.
In Isabelle theorem prover we use this
ASCII notation for First-Order Logic
Usually we treat formulas as syntax trees and not strings.
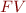 denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
\[\begin{array}{rcl}
denotes the set of free variables in the given propositional formula and can be defined recursively as follows:
\[\begin{array}{rcl}
FV(x) &=& \{ x \}, \mbox{ for } x \in V \\
FV(f(t_1,\ldots,t_n) &=& F(t_1) \cup \ldots \cup F(t_n) \\
FV(R(t_1,\ldots,t_n) &=& F(t_1) \cup \ldots \cup F(t_n) \\
FV(t_1 = t_2) &=& F(t_1) \cup F(t_2) \\
FV(\lnot F) = FV(F) \\
FV(F_1 \land F_2) = FV(F_1) \cup FV(F_2) \\
FV(F_1 \lor F_2) = FV(F_1) \cup FV(F_2) \\
FV(F_1 \rightarrow F_2) = FV(F_1) \cup FV(F_2) \\
FV(F_1 \leftrightarrow F_2) = FV(F_1) \cup FV(F_2) \\
FV(\forall x.F) = FV(F) \setminus \{x\} \\
FV(\exists x.F) = FV(F) \setminus \{x\}
\end{array}\]
If 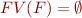 , we call
, we call  a closed formula.
a closed formula.