Exists-Forall Class (EPR, BSR) Definition
Also called Berneys-Schoenfinkel class and Effectively Propositional Logic (EPR).
Notation according to Classical Decision Problem classification: ![Math $[\exists^* \forall^*,all,(0)]_{=}$](/w/lib/exe/fetch.php?media=wiki:latex:/imgbf7e96575965b93cc9bd92240aa391a2.png)
That means: first-order logic sentences of the form 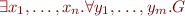 where
where  is quantifier-free formula with equality, with arbitrary relation symbols and constants, but without function symbols.
is quantifier-free formula with equality, with arbitrary relation symbols and constants, but without function symbols.
Summary of restrictions:
- only universal quantifiers (the initial existential ones get skolemized in satisfiability checking)
- no function symbols
Examples
For binary relations 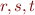 to express
to express  , we can introduce binary relation symbols
, we can introduce binary relation symbols  ,
,  ,
,  and write formula
and write formula
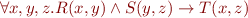
To express 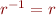 we would write
we would write
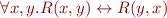
List contains no duplicates:
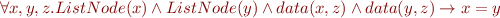
Relation  is a partial function
is a partial function
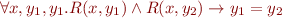
We cannot express in this class that  is a total function, or property like
is a total function, or property like 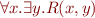 because we need an existential quantifier after a universal one.
because we need an existential quantifier after a universal one.