Classical Decision Problem
Consider satisfiability problem for sentences in first-order logic.
Without loss of generality, assume that formulas are in prenex form.
Classify formulas according to
- regular expression describing the sequence of quantifiers (e.g.
 means formulas
means formulas 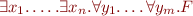 where
where  is quantifier-free)
is quantifier-free) - sequence of numbers of relation symbols for each arity
- sequence of numbers of function symbols for each arity
- presence or absence of equality in formulas
For each such description, determine whether the subsets of formulas that satisfy it are decidable or not.
Example: the exists-forall class that we will look at shortly is denoted ![Math $[\exists^* \forall^*,all,(0)]_{=}$](/w/lib/exe/fetch.php?media=wiki:latex:/imgbf7e96575965b93cc9bd92240aa391a2.png) .
.