Evaluating Formulas in Finite Structures
Recall semantic function definitions for First-Order Logic Semantics.
Suppose 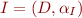 ,
,  is a finite set and
is a finite set and  is given by explicitly listing their values for all argument tuples (e.g. in a table).
is given by explicitly listing their values for all argument tuples (e.g. in a table).
Then evaluation functions 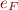 and
and 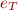 give algorithms to determine the truth value of
give algorithms to determine the truth value of  .
.
This is the model checking problem for first-order logic on finite structures: is a given interpretation model of  .
.
Applications of Formula Evaluation
Uses of this algorithm: state of a software system is given as interpretation  .
.
- database constraint integrity checking
- run-time checking
Example: Checking Database Integrity Constraint
Database integrity constraint:
ALL studentID. ALL courseID. Registered(studentID,courseID) --> (EX courseName. courseCatalog(courseID, courseName))
Example: Checking Assertion in Program with Heap
List contains no duplicates:
ALL n1. ALL n2. ListNode(n1) & ListNode(n2) & data(n1)=data(n2) --> n1=n2
Efficiency of Evaluating Formulas
Given a language  , formula a formula
, formula a formula  in
in  and an interpretation
and an interpretation 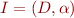 , determine
, determine 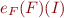 .
.
Basic idea: to evaluate quantifiers, iterate over all domain elements.
- fix formula, change domain size
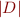 : LOGSPACE (number of vars fixed, number of their bits changes)
: LOGSPACE (number of vars fixed, number of their bits changes) - fix language with symbols of bounded arity, change formula: PSPACE (number of variables increases with formula size, see also QBF)
References
- Neil Immerman: Descriptive Complexity, Springer