LARA

This is an old revision of the document!

Definition of Set Constraints

Set constraints are a logic used in program analysis. In set constraints, each variable denotes a set of ground terms.

Let $L$ be a language of function symbols and constants. We write $f \in L$ for an element of $L$. Let $GT$ be the set of ground terms in language $L$.

Syntax of Set Constraints

\[ \begin{array}{l} 

S ::= v | S \cap S | S \cup S | S \setminus S | f(S, ..., S) | f^{-i}(S) \\
F ::= S \subseteq S \mid F \land F

\end{array} \] where

  • $v$ - set variable
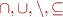  • $\cap,\cup,\setminus,\subseteq$ - standard set operations and relations
  • $f \in L$ - function symbol
  • in 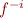$f^{-i}$, $i$ is an integer between 1 and arity of $f$

Semantic

  • $v$ - set variable, subset of $GT$
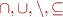  • $\cap,\cup,\setminus,\subseteq$ - standard set operations and relations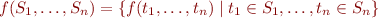
  • $f(S_1,\ldots,S_n) = \{ f(t_1,\ldots,t_n) \mid t_1 \in S_1,\ldots, t_n \in S_n \}$
  • $f^{-i}(S) = \{ t_i \mid f(t_1,\ldots,t_n) \in S \}$

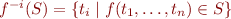
Example1

\[ 

  f(\{a,f(b,b)\},\{b,c\}) = \{ f(a,b),f(a,c),f(f(b,b),b), f(f(b,b),c) \}

\]

Example2

\[ 

  f^{-2}(\{a,f(a,b),f(f(a,a),f(c,c))\}) = \{b,f(c,c)\}

\]

Example3

What is the least solution of constraints \[ \begin{array}{l} 

a \subseteq S \\
f(f(S)) \subseteq S

\end{array} \] where $a$ is constant and $f$ is unary function symbol.

Example4

What is the least solution of constraints \[ \begin{array}{l} 

a \subseteq S \\
black(S) \subseteq S \\
red(black(S)) \subseteq S

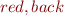\end{array} \] where $a$ is constant, $red,back$ are unary function symbols.

Example5

Let $L = \{a_1,\ldots,a_n, not, and, or, implies\}$ where

  • $a_1,\ldots,a_n$ are constants representing propositional constants
  • $not$ is unary function symbol representing negation in abstract syntax tree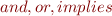
  • $and,or,implies$ are binary function symbols representing $\land,\lor,\rightarrow$ in syntax tree

Then the set of ground terms $GT$ represents propositional formulas.

What does the least solution of these constraints represent (where $S$,$P$ are set variables): \[ \begin{array}{l} 

a_1 \subseteq P \\
\ldots \\
a_n \subseteq P \\
P \subseteq S \\
not(P) \subseteq S \\
and(S,S) \subseteq S \\
or(S,S) \subseteq S

\end{array} \]

Existence of Solutions

Conditional Constraints

An important property we would like to have in this semantic is a very intuitive one : \[ f^{-1}(f(S_1, S_2)) = S_1 \] This property is in fact not conserved as we can easily see using a very simple counter-example : \[ f^{-1}(f(S_1, \emptyset)) = t_1 \in [[S_1 \wedge t_2 \in \emptyset \rbrace)]] = f^{-1}(\emptyset) = \emptyset \]

The correct interpretation of this property is :

\begin{displaymath} [[f^{-1}(f(S_1, S_2))]] = \left\{ \begin{array}{ll} \emptyset & if [[S_2]] = \emptyset & [[S_1]] & otherwise \\ \end{array} \right \end{displaymath}