This is an old revision of the document!
Complete Recursive Axiomatizations
Theorem: Let a set of formulas  be a recursive axiomatization for a complete and consistent theory, that is:
be a recursive axiomatization for a complete and consistent theory, that is:
 is recursive: there exists a an algorithm for checking, given
is recursive: there exists a an algorithm for checking, given  , whether
, whether 
 is complete: for each FOL sentence
is complete: for each FOL sentence  , either
, either  or
or 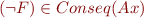
Then there exists an algorithm for checking, given  , whether
, whether  .
.
In other words, if a complete theory has a recursive axiomatization, then this theory is decidable.
(Note: a finite axiomatization is recursive. Typical axiomatizations that use “axiom schemas” are also recursive.)
Conversely: if a theory is undecidable (there is no algorithm for deciding whether a sentence is true or false), then the theory does not have a recursive axiomatization.
Proof.
Suppose  is a complete recursive axiomatization. There are two cases, depending on whether
is a complete recursive axiomatization. There are two cases, depending on whether  is consistent.
is consistent.
Case 1): The set  is inconsistent, that is, there are not models for
is inconsistent, that is, there are not models for  . Then
. Then  is the set of all first-order sentences and there is a trivial algorithm for checking whether
is the set of all first-order sentences and there is a trivial algorithm for checking whether  : always return true.
: always return true.
Case 2): The set  is consistent. Given
is consistent. Given  , to check whether
, to check whether  we run in parallel two complete theorem provers (which exist by Herbrand theorem), the first one trying to prove the formula
we run in parallel two complete theorem provers (which exist by Herbrand theorem), the first one trying to prove the formula  , the second one trying to prove the formula
, the second one trying to prove the formula  ; the procedure terminates if any of these theorem provers succeed. We show that this is an algorithm that decides
; the procedure terminates if any of these theorem provers succeed. We show that this is an algorithm that decides  .
.
- Because either
 or
or 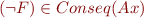 and theorem provers are complete one of these theorem provers will eventually halt. The procedure is therefore an algorithm.
and theorem provers are complete one of these theorem provers will eventually halt. The procedure is therefore an algorithm. - If
 is proved, then by soundness of theorem prover,
is proved, then by soundness of theorem prover,  .
. - If
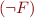 is proved, then by soundness of theorem prover
is proved, then by soundness of theorem prover 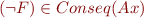 . Because
. Because  is consistent, there is a model
is consistent, there is a model  for
for  . Then
. Then 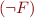 is true in
is true in  , so
, so  is false in
is false in  . Because there is a model where
. Because there is a model where  does not hold, we have
does not hold, we have  .
.
End of Proof.
Example: the theory of integers with multiplication and quantifiers is undecidable
- consequently, there are no complete axiomatizations for it, no decidable set of axioms from which the truth value of facts about natural numbers follows
- this result is one part of Goedel's incompleteness theorem