Abstract Interpretation
Goal: Invariant Inference by Approximation
Approximate strongest postcondition 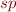 with operator
with operator  whose fixedpoint e.g. has a finite height.
whose fixedpoint e.g. has a finite height.
Let PS denote program states and 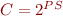 denote the set of all subsets of PS, so
denote the set of all subsets of PS, so 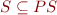 and
and  for a set of states S. We introduce an abstract analysis domain A and functions
for a set of states S. We introduce an abstract analysis domain A and functions

Instead of working with C, we work with simpler domain A, which is the data structure for analysis.
Examples of A:
- mapping from variables to information about the values they can have (interval analysis, sign analysis, constant propagation)
- formula F (usually in canonical form) such that
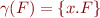
So, we will impose that our domain is partial order. It is useful to require additional property, namely that we have lattice, which have “union”-like and “intersection”-like operations.
Note that  allows us to define set-like operations on A that correspond to operations on A:
allows us to define set-like operations on A that correspond to operations on A:
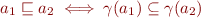
Instead of  , we have its approximation
, we have its approximation 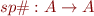 . To be sound we need to have
. To be sound we need to have
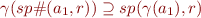
This is the most important condition for abstract interpretation.
One way to find  it is to have
it is to have  that goes the other way
that goes the other way

such that
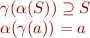
Then we can write a definition of 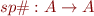 in terms of it:
in terms of it:
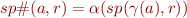
and we call this “the best transformer”.
Abstract computation of program semantics
In our lattice we have

because of the way we defined order.
Consider first only a single loop.
Then we rewrite our computation of sp for the loop by replacing 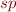 with
with  and replacing
and replacing  with
with  . We obtain fixpoint equation for computing the effect of a transitive closur eof a relation (i.e. a loop):
. We obtain fixpoint equation for computing the effect of a transitive closur eof a relation (i.e. a loop):
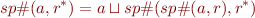
We can then iterate this equation until it stabilizes.
From the properties of  it follows that the result is approximation of the set of reachable states.
it follows that the result is approximation of the set of reachable states.
When does it stabilize? Note that the sequence is increasing and if we ever repeat we have stabilized. If there are no infinite ascending chains, the computation terminates.
References
- Calculus of Computation Textbook, Chapter 12 on invariant generation