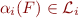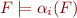A Simple Sound Combination Method
The following method need not be complete, but applies to any formulas, not just quantifier-free formulas.
Suppose we wish to unsatisfiability of a class of formulas  and we have provers
and we have provers  which can prove formulas in language
which can prove formulas in language  for
for 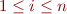 .
.
Suppose each prover has approximation function  such that
such that
In other words,  approximates an arbitrary formula with a weaker formula in language understood by
approximates an arbitrary formula with a weaker formula in language understood by  .
.
To prove formula  , for each
, for each  , apply
, apply  to check satisfiability of
to check satisfiability of 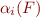 .
.
- If any of the provers concludes that formula is unsatisfiable, then
 is unsatisfiable (soundness)
is unsatisfiable (soundness) - If no prover finds unsatisfiability, we cannot say much in general, depending on the approximation functions
Improvement of precision: if  is equivalent to disjunction
is equivalent to disjunction 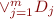 then to prove
then to prove  unsatisfiable, for each
unsatisfiable, for each 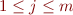 check that
check that 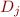 is unsatisfiable by applying each of the provers.
is unsatisfiable by applying each of the provers.
Defining Approximations
We can define approximation for arbitrary first-order formulas.
Start with 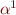 , flip on negation.
, flip on negation.
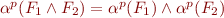
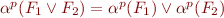
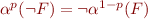
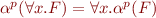
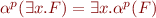
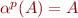 for any supported atomic formula
for any supported atomic formula
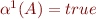 for unsupported atomic formula
for unsupported atomic formula
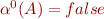 for unsupported atomic formula
for unsupported atomic formula
Lemma: 
What does 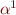 do on a conjunction of flat literals?
do on a conjunction of flat literals?
Examples
Consider decision procedure 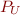 for uninterpreted symbols and
for uninterpreted symbols and  for Presburger arithmetic. Let approximation
for Presburger arithmetic. Let approximation 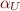 convert formula to negation normal form, and then drop all literals that contain arithmetic elements. Similarly,
convert formula to negation normal form, and then drop all literals that contain arithmetic elements. Similarly,  converts to NNF, then drops all literlas that contain symbols not presented in Presburger arithmetic (e.g. uninterpreted function symbols).
converts to NNF, then drops all literlas that contain symbols not presented in Presburger arithmetic (e.g. uninterpreted function symbols).
Example (from Calculus of Computation Textbook, page 210, Example 10.1): Let  be
be
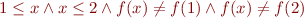
This formula is unsatisfiable. However,
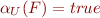

and both approximations are satisfiable in resulting theories.
Instead of doing approximation directly, let us transform the original formula into formula  where function application and arithmetic are separated:
where function application and arithmetic are separated:

Variables  and
and 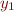 both appear in the formula, so let us convert
both appear in the formula, so let us convert  into disjunction of
into disjunction of  . We then check satisfiability for each of the disjuncts. Consider, for example,
. We then check satisfiability for each of the disjuncts. Consider, for example,  , which is formula
, which is formula 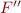
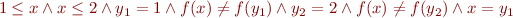
We have
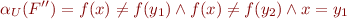
which is unsatisfiable. Then, considering formula  , we can do further case analysis on equality of two variables, say
, we can do further case analysis on equality of two variables, say 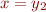 . For
. For 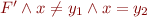 we similarly obtain unsatisfiability of
we similarly obtain unsatisfiability of 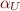 -approximation. The remaining case is
-approximation. The remaining case is 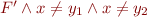 . For this formula, denoted
. For this formula, denoted 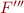 , we have
, we have
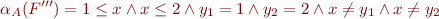
which is unsatisfiable. Therefore, by transforming formula into disjunction of formulas, we were able to prove unsatisfiability. Two things helped precision
- separating literals into literals understood by individual theories (unlike mixed literals
 )
) - doing case analysis on equality of variables
These are the key techniques that we use in methods that are complete for quantifier-free combinations of procedures that reason about disjoint function and predicate symbols.