Standard-Model Semantics of HOL
Frame
Generalizing domain set  of FOL and a family of domains
of FOL and a family of domains  for each sort
for each sort  in multisorted logic, in HOL we have one domain
in multisorted logic, in HOL we have one domain  for each type
for each type  (including structured types).
(including structured types).
We require that 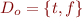 and we call its elements truth values. We call elements of
and we call its elements truth values. We call elements of  individuals. We require that
individuals. We require that 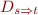 is a subset of the set of all total from
is a subset of the set of all total from  to
to  .
.
(If 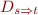 contains all total functions from
contains all total functions from  to
to  , we are talking about a standard model.)
, we are talking about a standard model.)
Such a collection of  for each
for each  is called a frame.
is called a frame.
Interpretation
An interpretation consists of frames  for each type
for each type  , and a function
, and a function  that maps constants to elements of appropriate sets in the frames.
that maps constants to elements of appropriate sets in the frames.
We require that  map constant
map constant  into (curried) equality relation on the set
into (curried) equality relation on the set  . That is, it is a function that, given
. That is, it is a function that, given  , returns a characteristic function
, returns a characteristic function 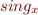 of the singleton set
of the singleton set  , given by
, given by
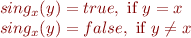
On the other hand, we require  to be some choice function, which has the property that
to be some choice function, which has the property that 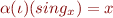 . Note that
. Note that  is defined for other functions as well, but we do not specify how it should behave on such functions.
is defined for other functions as well, but we do not specify how it should behave on such functions.
Assignment
Whereas  maps values of equalities and the choice function, an assignment
maps values of equalities and the choice function, an assignment  maps values of variables, mapping each variable of type
maps values of variables, mapping each variable of type  into element of
into element of  .
.
General Model
We call an interpretation 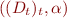 a general model if there exists a meaning function
a general model if there exists a meaning function  mapping each term of type
mapping each term of type  to element of
to element of  such that for all interpretations
such that for all interpretations  the following holds:
the following holds:
![Equation \begin{equation*}\begin{array}{l}
e(\varphi)(x) = \varphi(x) \\
e(\varphi)(c) = \alpha(c) \mbox{ i{}f } c \mbox { is a constant } \\
e(\varphi)(F_1 F_2) = (e(\varphi)(F_1))(e(\varphi)(F_2)) \mbox{ (evaluate both arguments, perform function application) }\\
e(\varphi)(\lambda x_t. B) = f \mbox{ where } f(v) = e(\varphi[x:=v])(B) \mbox{ for all } v \in D_t
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgf0fe3fea896760f59dc1165960d9ebc4.png)
If such interpretation function  exists, then it is unique. The reason it may not exist is only if
exists, then it is unique. The reason it may not exist is only if  for some
for some  does not have sufficiently many elements so that
does not have sufficiently many elements so that 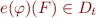 . But for standard model this is not a concern, and in such case the meaning is what we would expect, with lambda terms denoting total functions and quantification denoting quantification over all functions.
. But for standard model this is not a concern, and in such case the meaning is what we would expect, with lambda terms denoting total functions and quantification denoting quantification over all functions.
Standard Model
We will focus on standard models in this lecture; they correspond to our expected interpretation of HOL, but they do not have an enumerable set of axioms. If we allow non-standard models (where only some of the functions in 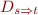 exist, that is, at least those that have names), then we can have an enumerable set of axioms, but then we allow small models (like Herbrand models in FOL). This is very analogous to what happens when we add axioms to FOL and consider theories of integers or set theory: we must accept either non-standard models or non-effetive axiomatization. HOL is in fact similar to having FOL with some extra axioms.
exist, that is, at least those that have names), then we can have an enumerable set of axioms, but then we allow small models (like Herbrand models in FOL). This is very analogous to what happens when we add axioms to FOL and consider theories of integers or set theory: we must accept either non-standard models or non-effetive axiomatization. HOL is in fact similar to having FOL with some extra axioms.