LARA

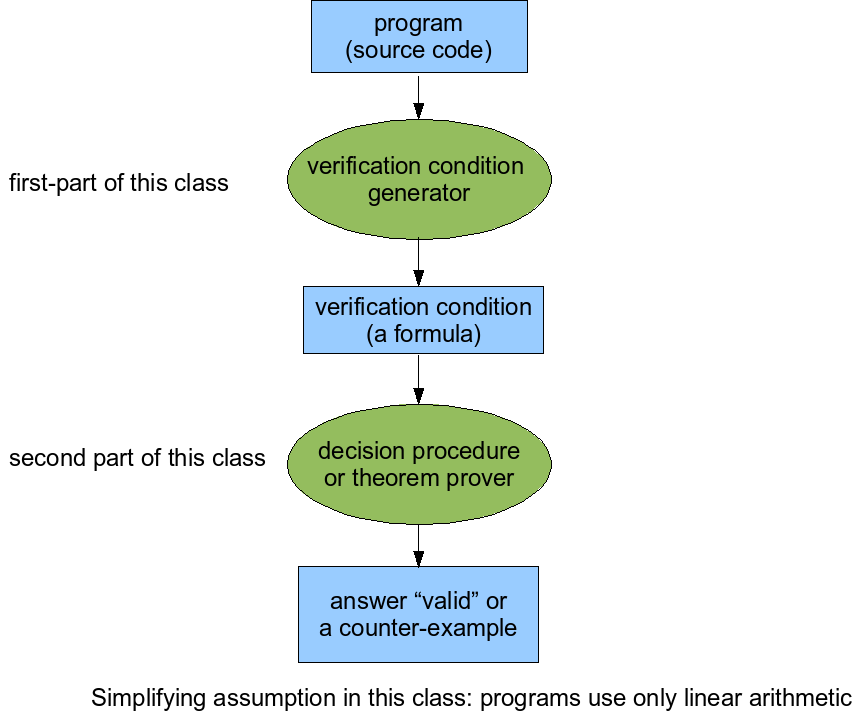
Lecture 3 (Skeleton)

Summary of what we are doing in today's class:

Verification condition generation: converting programs into formulas

Context

Recall that we can

  • represent programs using guarded command language, e.g. desugaring of 'if' into non-deterministic choice and assume
  • give meaning to guarded command language statements as relations
  • we can represent relations using set comprehensions; if our program c has two state components, we can represent its meaning R( c ) as 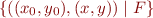$\{((x_0,y_0),(x,y)) \mid F \}$, where F is some formula that has x,y,x_0,y_0 as free variables.
  • simple values: variables are integers. Later we will talk about modeling pointers and arrays, but what we say now applies

Our goal is to find rules for computing R( c ) that are

  • correct
  • efficient
  • create formulas that we can effectively prove later

What exactly do we prove about the formula R( c ) ?

We prove that this formula is valid: 

R( c ) -> error=false

Formulas for basic statements

In our simple language, basic statements are assignment, havoc, assume, assert. 

R(x=t) = (x=t & y=y_0 & error=error_0)

Note: all our statements will have the property that if error_0 = true, then error=true. That is, you can never recover from an error state. This is convenient: if we prove no errors at the end, then there were never errors in between.

Note: the condition y=y_0 & error=error_0 is called <b>frame condition</b>. There are as many conjuncts as there are components of the state. This can be annoying to write, so let us use shorthand frame(x) for it. The shorthand frame(x) denotes a conjunction of v=v_0 for all v that are distinct from x (in this case y and error). We can have zero or more variables as arguments of frame, so frame() means that nothing changes. 

R(havoc x) = frame(x)
R(assume F) = F[x:=x_0, y:=y_0, error:=error_0] & frame()
R(assert F) = (F -> frame)

Note: 

x=t  is same as  havoc(x);assume(x=t)
assert false = crash  (stops with error)
assume true  = skip   (does nothing)

Composing formulas using relation composition

This is perhaps the most direct way of transforming programs to formulas. It creates formulas that are linear in the size of the program.

Non-deterministic choice is union of relations, that is, disjunction of formulas: 

CR(c1 [] c2) = CR(c1) | CR(c2)

In sequential composition we follow the rule for composition of relations. We want to get again formula with free variables x_0,y_0,x,y. So we need to do renaming. Let x_1,y_1,error_1 be fresh variables. 

CR(c1 ; c2) = exists x_1,y_1,error_1.  CR(c1)[x:=x_1,y:=y_1,error:=error_1] & CR(c2)[x:=x_1,y:=y_1,error:=error_1]

The base case is 

CR(c)=R(c)

when c is a basic command.

Avoiding accumulation of equalities

This approach generates many variables and many frame conditions.

Ignoring error for the moment, we have, for example: 

R(x=3) = (x=3 & y=y_0)
R(y=x+2) = (y=x_0 + 2 & x=x_0)
CR(x=3;y=x+2) = x_1=3 & y_1 = y_0 & y = x_1 + 2 & x = x_1

But if a variable is equal to another, it can be substituted using the substitution rules 

(exists x_1. x_1=t & F(x_1))     <->    F(t)
(forall x_1. x_1=t -> F(x_1)     <->    F(t)

We can apply these rules to reduce the size of formulas.

Approximation

If (F → G) is value, we say that F is stronger than F and we say G is weaker than F.

When a formula would be too complicated, we can instead create a simpler approximate formula. To be sound, if our goal is to prove a property, we need to generate a *larger* relation, which corresponds to a weaker formula describing a relation, and a stronger verification condition. (If we were trying to identify counterexamples, we would do the opposite).

We can replace “assume F” with “assume F1” where F1 is weaker. Consequences:

  • omtiting complex if conditionals (assuming both branches can happen - as in most type systems)
  • replacing complex assignments with arbitrary change to variable: because x=t is havoc(x);assume(x=t) and we drop the assume

This idea is important in static analysis.

Symbolic execution

Symbolic execution converts programs into formulas by going forward. It is therefore somewhat analogous to the way an interpreter for the language would work.

Avoid renaming all the time. 

SE(F,k, c1; c2) = SE(F & R(c1), k+1, c2)             (update formula)
SE(F,k,(c1 [] c2); c2) = SE(F, k, c1) | SE(F,k,c2)   (explore both branches)

Note: how many branches do we get?

Strongest postcondition:

\begin{equation*} sp(P,r) = \{ s_2 \mid \exists s_1.\ s_1 \in P \land (s_1,s_2) \in r \} \end{equation*}

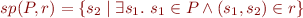
Like composition of a set with a relation. It's called relational image of set $P$ under relation $r$.

Note: when proving our verification condition, instead of proving that semantics of relation implies error=false, it's same as proving that the formula for set sp(U,r) implies error=false, where U is the universal relation, or, in terms of formulas, computing the strongest postcondition of formula 'true'.

Weakest preconditions

While symbolic execution computes formula by going forward along the program syntax tree, weakest precondition computes formula by going backward. 

wp(Q, x=t) =
wp(Q, assume F) =
wp(Q, assert F) =
wp(Q, c1 [] c2) = 
wp(Q, c1 ; c2) =

Inferring Loop Invariants

Suppose we compute strongest postcondition in a program where we unroll loop k times.

  • What does it denote?
  • What is its relationship to loop invariant?

Weakening strategies

  • maintain a conjunction
  • drop conjuncts that do not remain true

Alternative:

  • decide that you will only loop for formulas of restricted form, as in abstract interpretation and data flow analysis (next week)

One useful decision procedure: Proving quantifier-free linear arithmetic formulas

Suppose that we obtain (one or more) verification conditions of the form

\begin{equation*} F\ \rightarrow\ (\mbox{error}=\mbox{false}) \end{equation*}

whose validity we need to prove. We here assume that F contains only linear arithmetic. Note: we can check satisfiability of $F\ \land\ (\mbox{error}=\mbox{true})$. We show an algorithm to check this satisfiability.

Quantifier Presburger arithmetic

Here is the grammar: 

var = x | y | z | ...                    (variables)
K = ... | -2 | -1 | 0 | 1 | 2 | ...      (integer constants)
T ::= var | T + T | K * T                (terms)
A ::= T=T | T <= T                       (atomic formulas)
F ::= A  |  F & F |  F|F  |  ~F          (formulas)

To get full Presburger arithmetic, allow existential and universal quantifiers in formula as well.

Note: we can assume we have boolean variables (such as 'error') as well, because we can represent them as 0/1 integers.

Satisfiability of quantifier-free Presburger arithmetic is decidable.

Proof: small model theorem.

Small model theorem for Quantifier-Free Presburger Arithmetic (QFPA)

First step: transform to disjunctive normal form.

Next: reduce to integer linear programming:

\begin{equation*} A\vec x = \vec b, \qquad \vec x \geq \vec 0 \end{equation*}

where $A \in {\cal Z}^{m,n}$ and $x \in {\cal Z}^n$.

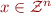Then solve integer linear programming (ILP) problem

We can prove small model theorem for ILP - gives bound on search.

Short proof by Papadimitriou:

  • solution of Ax=b (A regular) has as components rationals of form p/q with bounded p,q
  • duality of linear programming
  • obtains bound $M = n(ma)^{2m+1}$, which needs $\log n + (2m+1)\log(ma)$ bits
  • we could encode the problem into SAT: use circuits for addition, comparison etc.

Note: if small model theorem applies to conjunctions, it also applies to arbitrary QFPA formulas.

Moreover, one can improve these bounds. One tool based on these ideas is UCLID.

Alternative: enumerate disjuncts of DNF on demand, each disjunct is a conjunction, then use ILP techniques (often first solve the underlying linear programming problem over reals). Many SMT tools are based on this idea (along with Nelson-Oppen combination: next class).

  • CVC3 (successor of CVC Lite)
  • SMT-LIB Standard for formulas, competition

Full Presburger arithmetic

Full Presburger arithmetic is also decidable.

Approaches:

  • Quantifier-Elimination (Omega tool from Maryland) - see homework
  • Automata Theoretic approaches: LASH, MONA (as a special case)

Papers