Lecture 2

Manually proving an example

Recall our example from Lecture 1, with a loop invariant:

    public static int sum(int a0, int n0)
   /*:
     requires "a0 > 0 & n0 > 0"
     ensures "result > 0"
   */
    {
        int res = 0, a = a0, n = n0;
        while //: inv "a > 0 & res >= 0 & (n = n0 | res > 0)"
            (n > 0)
        {
            a = 2*a;
            res = res + a;
            n = n - 1;
        }
        return res;
    }

What formulas do we need to prove?

Two questions:

why is this correct
how do we automate it?

To answer the first question, we first need to define semantics of programs.

Logical preliminaries

We used these constructs in mathematics all the time. Formalizing them is useful for

foundation of mathematics (first half of 19th century)
proving formulas automatically: need to represent formulas and make correct reasoning steps on them

Propositional logic

Basic propositional operations: $\land, \lor, \lnot, \rightarrow, \leftrightarrow$

Context-free grammar for propositional logic.

Example formula:

$((p \rightarrow q) \land (\lnot p \rightarrow r)) \leftrightarrow ((p \land q) \lor (\lnot p \land r))$

Is “false implies true” valid formula?

There is an algorithm that checks whether a formula is

satisfiable
valid

What is the algorithm?

SAT solvers: http://www.satlive.org/

First-order logic (predicate calculus)

Predicate: a function from some arguments into true or false.

Example: “p divides q” is a binary predicate on p and q.

Predicate calculus is concerned with properties of predicates (regardless of what these predicates are).

Constructs in predicate calculus:

$\forall, \exists, P(t_1,t_2), t_3=f(t_4)$

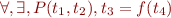
Context-free grammar for first-order logic.

Drinker's paradox (made more politically correct): in every restaurant there is a guest such that if this guest is having a dessert, then everyone in the restaurant is having a dessert.

How to formalize it? Is it valid? Why?

Tarskian semantics for first-order logic.

Is there an algorithm for first-order logic?

Checking (and enumerating) proofs.

What is a formal proof?

Sets and relations

Constructs

$\begin{array}{l} \{ x_1,\ldots,x_n \} \\ \{ x \mid P(x) \} \\ \in, \cap, \cup, \subseteq, \times \end{array}$

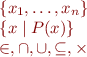
Example:

$\begin{array}{rcl} A &=& \{2,4,6\} \\ B &=& \{3,6\} \end{array}$

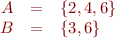
We will use binary relations on program states to represent the meaning of programs. A binary relation on set S is a subset of

$S \times S$

Diagonal is

$\Delta_S = \{(x,x) \mid x \in S \}$

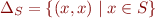
Because relation is a set, all set operations apply. In addition, we can introduce relation composition, denoted by circle

$r \circ s = \{(x,z) \mid \exists y.\ (x,y) \in r \land (y,z) \in s \}$

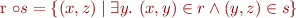
Then

$r^n = r \circ \ldots \circ r \ \ \ \ \mbox{($n$ times)}$

$r^* = \Delta_S \cup r \cup r^2 \cup r^3 \cup \ldots$

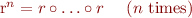
Sets and properties are interchangable.

$x \in P$ turns set into predicate.

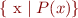$\{ x \mid P(x)\}$ turns predicate into a set.

$\{ x \mid P_1(x) \} \cap \{ x \mid P_2(x) \} = \{ x \mid P_1(x) \land P_2(x) \}$

$(x \in S_1 \cap S_2) \leftrightarrow (x \in S_1 \land x \in S_2)$

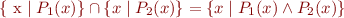
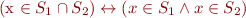
Programs as relations

Now back to meaning of programs.

Simple programming language

x = exp
if (F) c1 else c2
c1 ; c2
while (F) c1

Consider a program that manipulates two integer variables.

What is the state - map from names to values.

What is the meaning of

x=y+3
x=x+y
x=y+3 ; x=x+y

Programs as formulas

Can we represent relations symbolically?

In general? In our examples?

$r = \{s \mid F(s(x),s(y)) \}$

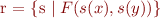
Accumulation of equalities.

Guarded command language

Our simple language:

x = exp
if (F) c1 else c2
c1 ; c2
while (F) c1

Guarded command language:

assume(F)
c1 [] c2
c1 ; c2
assert(F)
havoc(x)
c1*

Relational semantics of guarded commands.

Transforming language into guarded commands:

conditionals:

if (F) c1 else c2

⇒

(assume(F); c1)  []
(assume(~F); c2)

loops:

while (F) c1

⇒

(assume(F); c1)*; 
assume(~F)

loops, if we have loop invariants

while [inv I] (F) c1

⇒

assert(I);
havoc x1,...,xn;
assume(I);
(assume(~F) []
 assume(F);
 c1;
 assert I;
 assume(false));

Transformations such as these are used in Jahob, ESC/Java, Spec#.

Weakest Preconditions

Weakest precondition of a set of states is the

$wp(r,P) = \{ s_1 \mid \forall s_2. (s_1,s_2) \in r \rightarrow s_2 \in P \}$

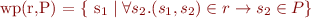
What happens if r is deterministic (a function on states)?

Set of states - formula with state variables for one state.

Relation on states - formula with state variables for two states.

Important property: conjunctivity.

$wp(r, P_1 \cap P_2) =$

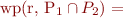
Weakest preconditions for guarded commands.

Weakest preconditions of assignments make wp very appealing.

Proving validity of linear arithmetic formulas

Quantifier-Free Presburger arithmetic

$\begin{array}{l} \land, \lor, \lnot, \\ x + y, K \cdot x, x < y, x=y \end{array}$

Validity versus satisfiability. For all possible values of integers.

Reduction to integer linear programming.

Small model property.

See, for example, paper by Papadimitriou.

If we know more about the structure of solutions, we can take advantage of it as in the paper by Seshia and Bryant.

Semantics of references and arrays

Program with class declaration

class Node {
   Node left, right;
}

How can we represent fields?

Possible mathematical model: fields as functions from objects to objects.

left : Node => Node
right : Node => Node

What is the meaning of assignment?

x.f = y

$f[x \mapsto y](z) = \left\{ \begin{array}{lr} y, & z=x \\ f(z), & z \neq x \end{array}\right.$

Eliminating function updates in formulas.

Representing arrays.

What does this mean for our formulas?

  assume (x.f = 1);
  y.f = 0;
  assert (x.f > 0)

left, right - uninterpreted functions (can have any value, depending on the program, unlike arithmetic functions such as +,-,* that have fixed interpretation).

Reasoning about uninterpreted function symbols

Essentially: quantifier-free first-order logic with equality.

What are properties of equality?

Congruence closure algorithm. Here is the original paper by Nelson and Oppen.