LARA

Lecture 7: Formulas as a unifying domain for static analysis

General setup

Analysis domain based on formulas and main operations:

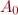  • $A_0$ - set of all first-order formulas (or other set closed under propositional operations and quantifiers)
  • $A \subseteq A_0$ - subset of formulas that we use as our analysis domain, e.g. finite. If we used abstract interpretation framework, we would have $\gamma(F)=\{st \mid [\![F]\!]st = \mbox{true}\}$
  • $N : A_0 \to A$ - normalization function, ensuring that the result is in our domain, works as $\alpha$ but goes from formulas to formulas
    • key requirement: 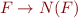$F \rightarrow N(F)$ is a valid formula ($N$ produces a weaker formula)
  • $sp : A_0 \times \mbox{Com} \to A_0$ - computes strongest postcondition on formulas precisely, e.g. $sp(F(x),R(x,y)) = \exists x_1. F(x_1) \land R(x_1,x)$.

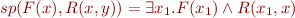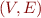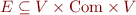Control-flow graph is graph $(V,E)$ where $V$ are program points (between statements) and $E \subseteq V \times \mbox{Com} \times V$ are edges labelled with program commands.

The state of our analysis (set of computed facts) maps program points to formulas in 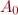$A_0$, that is: $\mbox{fact} : V \to A_0$.

Basic philosophy of the analysis: compute precise result whenever possibly, then apply $N$ to fit it into $A_0$.

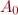Initial state: 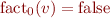$\mbox{fact}_0(v)=\mbox{false}$, except for initial program point 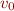$v_0$, where $\mbox{fact}_0(v_0)=\mbox{true}$ unless we know something about the initial program state.

  • intuition: computing abstraction of the set of reachable states

Update rule:

\begin{equation*} \mbox{fact}_{i+1}(v) := N(\mbox{fact}_i(v) \vee \bigvee { sp(\mbox{fact}_i(u),c) \mid (u,c,v) \in E \} ) \end{equation*}

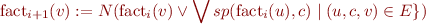
  • compute the impact of all incoming edges

Correctness: if for each program point 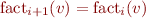$\mbox{fact}_{i+1}(v)=\mbox{fact}_i(v)$ for all $v \in V$, then the facts are true in all program executions.

(If we stopped the analysis before this happens, then the result is not correct, it does not take into account all executions).

Termination

  • observe the sequence of formulas 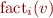$\mbox{fact}_i(v)$ for $0 \leq i$
  • start from false, become weaker and weaker
  • require that there are no infinite ascending chains of weaker and weaker formulas

Examples

Conjunctions of fixed predicates as analysis domain

Disjunctions of conjunctions of predicates

Comparison of precision and efficiency.

More in

Linear inequalities

Example implementation: Parma Polyhedra Library and a paper about Parma.

Special cases:

  • constant propagation
  • interval analysis
  • octagon domain

Simple pointer analysis

Consider constant field propagation with 

x = new Node();
y = new Node();
x.f = 1;
y.f = 2;

or with 

y = x.next;
x.f = 1;
y.f = 2;

Allocation-site based analyses