Lecture 20: Interprocedural Analysis - Introduction
intraprocedural analysis = analysis for language without procedures
interprocedural analysis = analysis for language with procedures
Given intraprocedural analysis, how do we create interprocedural analysis?
Assumptions
- No concurrency
- Only global variables
- No parameters
The last two assumptions are made for simplicity, since parameter passing can be simulated using global variables and assignments. For example, a function called p with a parameter x, p(x), can be represented as a function without parameters, p'(), by introducing a global variable x.
Example
proc main() {
p1();
p2();
}
proc p1() {
open();
readContent();
}
proc p2() {
startLog();
readContent();
stopLog();
close();
}
proc readContent() {
while (...) {
read();
print();
}
}
Desired properties
These are stated as regular expressions so that it is easier to check whether the program satisfies these constraints.
- must follow protocol: (open (read+write)* close)*
- must follow protocol: (startLog stopLog)*
Semantics for language with procedure calls
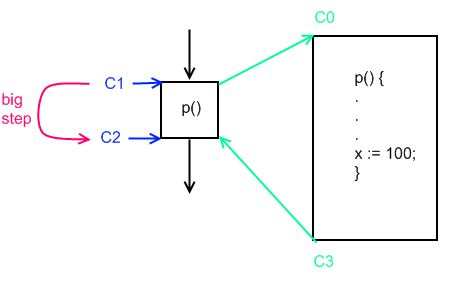
Big step
In this approach, we treat a procedure call as one step. This can be thought of like a step-over move in a debugger.
Let  be the set of program states and
be the set of program states and  be the set of vertices in the control flow graph. Then we can describe a point in the program as:
be the set of vertices in the control flow graph. Then we can describe a point in the program as:
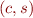
where 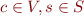
Consider the following example:
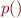 is a procedure which can described by the relation
is a procedure which can described by the relation  :
: 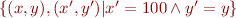
Then we can formally define the semantics of a big step ( ) as:
) as:

where 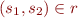 iff
iff 
Small step
Using small step semantics, we treat the procedure call as a sequence of small steps corresponding to each statement in the procedure. This is like the step-into move in a debugger. To accomplish this, we need a stack to keep track of the return point after we come back from a procedure. Therefore a program point can now be described as:

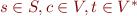
Here  is the set of sequences of vertices in the control flow graph.
is the set of sequences of vertices in the control flow graph.
Using the preceding example, the small steps ( ) can be described as:
) can be described as:

After the first step at the point where the procedure is entered,  is pushed on the stack so that we know where to return to after the procedure is done. The last step is the point where we return from the procedure, so we pop
is pushed on the stack so that we know where to return to after the procedure is done. The last step is the point where we return from the procedure, so we pop  from the stack and that is the point in the control flow graph where we return to.
from the stack and that is the point in the control flow graph where we return to.
Here we have assumed the procedure has no local variables, although to support them, we'd just need to add another set to the program description:
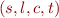
Here  , where
, where  is the set of mappings of local variables of a procedure to their values. Furthermore, on each procedure call, the program pushes
is the set of mappings of local variables of a procedure to their values. Furthermore, on each procedure call, the program pushes  on the stack along with the program point. Everything would be popped off from
on the stack along with the program point. Everything would be popped off from  when the procedure returns control to the callee.
when the procedure returns control to the callee.
One instance where small step semantics would be necessary is in concurrency, so that we can take into account interleaving.
Simple approaches to interprocedural analysis
Treat procedure calls as havoc statements
Assume the program is in an arbitrary state and model the procedure call as a havoc statement.
In previous lectures, we have seen how to compute
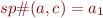
where  is a lattice and
is a lattice and 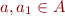 .
.
By treating a procedure call as a havoc, we would have
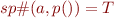
which would mean that anything can happen, and we would lose all precision.
However, we could still recover some properties if we have an intermediate step where the procedure call would be a havoc statement only on those variables declared in the modifies clause of the procedure. The problem with this approach is that it may be difficult to precisely define the modifies clause.
Inlining
When a procedure call is encountered, it is replaced by the statements of the procedure (so the procedure code is inlined with the code of the callee). A problem arises when the procedure being inlined is recursive. One approach to dealing with this situation is to inline the recursive procedure a few times, and then treat the recursive call as a havoc statement (as described above). However, even if this is done, inlining increases the size of the code exponentially.
Treat procedure calls as goto statements
Procedure calls are approximated with a goto statement, and return from a procedure is a non-deterministic goto statement (non-deterministic because the procedure could have been called from different places in the code, so there is no way to know where to return to). Consider the example program above, and the second property we would like it to satisfy:
(startLog stopLog)*
At the program point just before the first statement of the readContent() function, the value of the boolean variable stopLog is unknown, because we don't know whether the call was made by p1() or p2(). Therefore in order to check such properties, we would need a finite state automaton (FSA) to keep track of the value of the boolean variables.
Modular analysis with supplied contracts
During the verification of a program with procedures, when a procedure call is encountered, the procedure's contract is evaluated. We assume that the user has supplied the procedure contracts, although it may also be possible to infer contracts (especially the ensures clause).
In our example, to satisfy the second property of the program, we introduce a boolean variable
boolean loggingOn := false;
The procedure contract for p2() then looks like this:
requires: loggingOn = false modifies: loggingOn ensures: loggingOn = false
Now consider the first property:
(open (read+write)* close)*
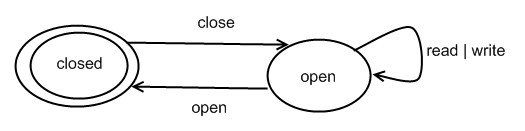
In order to define procedure contracts for readContent() and p1() to ensure that this property is satisfied, we introduce an object called FileState which has a typestate. In typestate systems, the type of an object is allowed to change during its lifetime in the computation. In the paper Generalized typestate checking for data structure consistency, it says that “unlike standard type systems, typestate systems can enforce safety properties that depend on changing object states”.
Therefore FileState has type file and two states, open and closed.
Using this notion, we can write the procedure contracts for the two methods as follows:
readContent() requires: FileState = open
p1() requires: FileState = closed modifies: FileState ensures: FileState = open
Analysis of regular properties of finite-state programs with stack (push down systems- PDS)
Assume we have a program with a finite number of program states. Recall that we can write a push down automata (PDA),  , which will accept a language,
, which will accept a language, 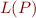 , that corresponds to all sequences of operations in the program (SAV07 Lecture 19). Then we can use the PDA to check whether the properties of the program (stated as regular expressions) hold. We do this by constructing a finite state automaton (FSA),
, that corresponds to all sequences of operations in the program (SAV07 Lecture 19). Then we can use the PDA to check whether the properties of the program (stated as regular expressions) hold. We do this by constructing a finite state automaton (FSA),  , which accepts the language,
, which accepts the language, 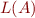 , corresponding to the regular expression for the property (recall the equivalence of finite state machine and regular expression languages). Then we verify whether the property holds by checking if the following is true:
, corresponding to the regular expression for the property (recall the equivalence of finite state machine and regular expression languages). Then we verify whether the property holds by checking if the following is true:

PDAs and context-free grammars (CFG) are equivalent. Therefore, as an example, we construct the CFG corresponding to the example program above:
 = {start, stop, open, read, close}
= {start, stop, open, read, close}
 is the set of symbols on the stack
is the set of symbols on the stack
 is the set of program states
is the set of program states
readContent ::= epsilon | read readContent p2 ::= start readContent stop close p1 ::= open readContent main ::= p1 p2
Now to check whether property 2 holds, we have to verify whether 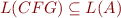 .
.
Checking whether one language is a subset of another
Recall that:
 iff
iff 
Therefore showing that  is true is equivalent to showing:
is true is equivalent to showing:
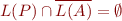
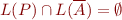
Let 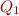 be the set of states of
be the set of states of  , and
, and  be the set of states of A. Then
be the set of states of A. Then 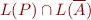 is the language accepted by a new PDA,
is the language accepted by a new PDA,  , whose set of states is
, whose set of states is  . Let
. Let  be the CFG equivalent to
be the CFG equivalent to  . Therefore the problem is now to check whether
. Therefore the problem is now to check whether 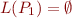 or equivalently whether
or equivalently whether 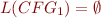
One way to do this is to systematically check the productions of  bottom up (starting from a terminal and following the non-terminals which are used to derive it). If the non-terminal representing the start symbol is reachable in at least one of the derivations, then
bottom up (starting from a terminal and following the non-terminals which are used to derive it). If the non-terminal representing the start symbol is reachable in at least one of the derivations, then 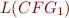 is non-empty, therefore
is non-empty, therefore 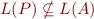 and the property that
and the property that  represents does not hold.
represents does not hold.
A formal analysis if this “reachability” problem in pushdown automata is discussed in the paper Reachability Analysis of Pushdown Automata: Application to Model Checking. A summary of the sections of the paper we covered in class are in the next section.
Convergence of automata for reachable configurations
One of the main results of this paper is an algorithm which, given a set of states  , computes the set of all predecessors of
, computes the set of all predecessors of  , denoted by
, denoted by 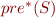 . The states in
. The states in 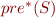 are regular, i.e. they can be represented using a finite state automaton.
are regular, i.e. they can be represented using a finite state automaton.
In the paper, a pushdown system is defined as a triplet 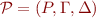 where
where
 is a finite set of control locations
is a finite set of control locations
 is a finite stack alphabet
is a finite stack alphabet
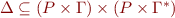 is a set of transition rules
is a set of transition rules
If 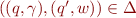 then we write
then we write 
Note: an input alphabet is not defined, since here we are only interested in the behavior of the PDS, not the specific language it accepts.
Multi-automata
Let 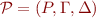 be a PDS with
be a PDS with 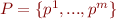 . A multi-automaton (MA for short) for
. A multi-automaton (MA for short) for 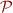 is a tuple
is a tuple  where
where
 is a finite set of states
is a finite set of states
 is a set of transitions
is a set of transitions
 is a set of initial states
is a set of initial states
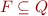 is a set of final states
is a set of final states
The transition relation  is defined as the smallest relation which satisfies the following properties
is defined as the smallest relation which satisfies the following properties
- if
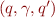 then
then 
 for every
for every 
- if
 and
and  then
then 
 accepts or recognizes a configuration
accepts or recognizes a configuration 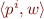 if
if  for some
for some  . The set of configurations recognized by
. The set of configurations recognized by  is denoted
is denoted 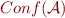 . As stated before, a set of configurations is regular if it recognized by some MA.
. As stated before, a set of configurations is regular if it recognized by some MA.
Section 2.2 of the paper explains how, given a regular set of configurations  of a PDS
of a PDS 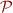 recognized by an MA
recognized by an MA  , we can construct another MA
, we can construct another MA  recognizing
recognizing 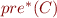 (refer to paper for details).
(refer to paper for details).
So the idea in the end is to make  include those undesirable (error) states, and then check whether
include those undesirable (error) states, and then check whether 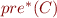 includes the starting state configurations (in other words, whether any of the error states are reachable from the start state).
includes the starting state configurations (in other words, whether any of the error states are reachable from the start state).
References
- M. Sharir, and A. Pnueli. Two Approaches to Inter-Procedural Data-Flow Analysis. In Jones and Muchnik, editors, Program Flow Analysis: Theory and Applications. Prentice-Hall, 1981.
- F. Nielson, H. R. Nielson, C. Hankin: Principles of program analysis, 2005. Chapter 2.5.
Continued in SAV07 Lecture 21.