Lecture 13: Concurrency
(See also SAV07 Lecture 26.)
A language with concurrency primitives
c ::= [r] | c[]c | c;c | c* | c||c | atomic(c)
[r] - havoc, assume, assert, assignments, any simple command, given by relation r
Examples
What are the possible results?
(x := 1; y := 1; z := x+y) || (y := 2; x := 12; z := x+y)
(x := 1; y := 1; z := x+y) || (y := 2; x := y+10; z := x+y)
For the above two programs, we assume that every statement is atomic. The above two programs result in different possible values for x, y and z. Consider the first program. When it terminates, the possible values for x, y and z are {(1,1,2), (12, 2, 14), (12, 1, 13)}. As for the second program, the possible values upon termination are {(1,1,2), (12, 2, 14), (12, 1, 13), (11,1,12)}. We note that the last possible valuation on (x,y,z) results from an interleaving of assignments where (y:=1) occurs between (y:=2) and (x:=y+10).
This suggests that the two programs above are not equivalent for the purpose of reasoning in concurrently executing programs.
A semantics of the language with concurrency
What would be the semantics of || as a composition of relations?
c ::= [r] | c[]c | c;c | c* | c||c | atomic(c)
We express the semantics of c, ![Math $[[c]] \subseteq 2^{R^*}$](/w/lib/exe/fetch.php?media=wiki:latex:/imga91d8b64f20662a792eb007e60a08291.png) as the set of all possible sequences of relations of c.
as the set of all possible sequences of relations of c.
![Math $[[c]] = { r_1^1 r_2^1 \ldots r_{n1}^1, r_1^2 r_2^2 \ldots r_{n2}^2, \ldots, r_1^l r_2^2 \ldots r_{nk}^k}$](/w/lib/exe/fetch.php?media=wiki:latex:/img9f58e37456dee0eaeb3bff953c03bd45.png) .
.
![Math $[[\, [r]\, ]] = \{ r \}$](/w/lib/exe/fetch.php?media=wiki:latex:/imgf70678998854282a400781a0cb8e271f.png)
![Math $[[C_1; C_2]] = [[C_1]] [[C_2]] = \{r_1 \ldots r_n s_1 \ldots s_m | r_i \in [[C_1]] and s_j \in [[C_2]] \}$](/w/lib/exe/fetch.php?media=wiki:latex:/img76b213c10b84e70a4c71029764edbdad.png) (This is similar to a language theoretic approach, where we express the concatenation of two languages
(This is similar to a language theoretic approach, where we express the concatenation of two languages 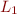 and
and  as
as
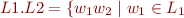 and
and 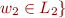 .
.
![Math $[[C_1 [] C_2 ]] = [[C_1]] \cup [[C_2]]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgd9f81b30b073d9b0d5be8be7f549d4b1.png) .
.
Let 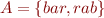 and
and 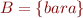 . Then
. Then 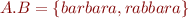 and
and  .
.
![Math $[[ C_1 || C_2 ]] = \bigcup {\{I(S_1,S_2)\}}$](/w/lib/exe/fetch.php?media=wiki:latex:/img0243c87a5b049fa26eaf920024d290c9.png) where
where ![Math $S_1 = [[C_1]]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgcfe1445c3395cd337cf2d9401e248389.png) and
and ![Math $S_2 = [[C_2]]$](/w/lib/exe/fetch.php?media=wiki:latex:/img68a11fbec5b1c10d41a86a7634589c45.png) , where
, where
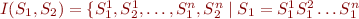 and
and 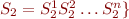 .
.
![Math $[[ C^* ]] = \cup_{n \ge 0} [[C^n]]$](/w/lib/exe/fetch.php?media=wiki:latex:/img4bc9a1cc56bf66de51c9cdfded26085d.png) where
where ![Math $[[C^0]] = \emptyset$](/w/lib/exe/fetch.php?media=wiki:latex:/img41690db5697f6a09b0d599f3cb828771.png) and
and ![Math $[[C^{n+1}]] = [[ C^n ; C]]$](/w/lib/exe/fetch.php?media=wiki:latex:/imgf502a05e72239d887f555e1552c72a53.png) .
.
 atomic
atomic![Math $(C) ]] = $](/w/lib/exe/fetch.php?media=wiki:latex:/img432ac5ca29276f66c6229e040f222af0.png) eval
eval![Math $([[C]])$](/w/lib/exe/fetch.php?media=wiki:latex:/img6d16f5c6690b8608fd516da59853560e.png) where eval is a function
where eval is a function 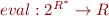 such that
eval
such that
eval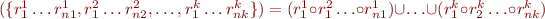 .
.
An example
{ b = x + y }
while (*) do
if (*) then
atomic{
x++;
y--;
}
else
atomic{
y++;
x--;
}
endif
end
||
while (*) do
if (*) then
atomic{
x++;
y--;
}
else
atomic{
y++;
x--;
}
endif
end
{ b = x + y }
In our language, this example can be expressed as
(atomic(x:=x+1;y:=y-1)[]atomic(x:=x-1;y:=y+1))* || (atomic(x:=x+1;y:=y-1)[]atomic(x:=x-1;y:=y+1))*
![Math $ = (r1[]r2)^*||(r3[]r4)^* \subseteq (r1 [] r2 [] r3 [] r4)^*$](/w/lib/exe/fetch.php?media=wiki:latex:/imgaff4c3447762f03568dc2e3a5bb149e0.png)
Global reachability invariants
Assume that atomic only applies to sequences of relations (so we treat them as biger atomic relations).
While theorem for parallel programs
(r1 [] ... [] rn)* || (r1 [] ... [] rn)* ||
While theorem when atomic is present - implementing atomic
- global lock
- transactions with state copying
Assume any set of states is expressible in our logic (allow set theory or FO logic with axioms).
Invariant for resulting while program is a global reachability invariant.
- good: only talks about current state
- bad: potentially refers to all components of parallel process
Alternative: complete history variables
- good: only talks about individual parallel process (except for join points)
- bad: refers not only to current, but also past states
Any point in between: introduce auxiliary variables, which can be local or global, whatever is best for the given program.
Example.
{x=0} (x:=x+1 || x:=x+10) {x=11}
Owicki-Gries method
Idea
- whenever modifying a group of shared variables (=resource), enforce certain invariants on those variables
- prevent interleavings within updates to variables of a resource
Examples: bytes of a word, nodes in a list
Parallel composition construct declares resources and starts parallel threads:
resource r1(vars1), ..., rn(varsn) cobegin S1 || ... || Sn coend
(Assume only one such top-level construct, for simplicity. Assume one resource.)
Accessing variables in a resource:
with r when B do S
Requirements:
- variable written in some process and used in another must be in a resource
- if a variable is in a resource, it can only be accessed using 'with' statement
Proof rules: introduce global invariant I for shared variables
{P & B & I} S {Q & I}
--------------------------
{P} with r when B do S {Q}
{P1} S1 {Q1}, ..., {Pn} Sn {Qn}
-------------------------------------------------------
{P1 & ... Pn & I} (S1 || ... || Sn) {Q1 & ... & Qn & I}
Requirements:
- variables in
 not modified outside
not modified outside 
Need for history variables.
Granularity of concurrency
Using concurrency for efficiency: trade off between sizes of atomic sections and ease of reasoning.
Theorems about equivalence can be used to verify less concurrent version, run more concurrent one.
Operational description of
with r when B do S
with lock per resouce:
atomic(assume r_available & B; r_available := false); S; r_available := true;
it by
atomic (assume B; S)
and replace cobegin with simple || under the assumptions of Owicki-Gries?
Transactions: a more abstract mechanism for atomicity, promises to get good point in reasoning/efficiency space.