Consider a fragment of Presburger arithmetic where atomic formulas are equalities or inequalities of the form , for arbitrary integer variables 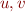and arbitrary constants .

F ::= A | (F&F) | (F|F) | ~F | ALL v.F | EX v.F
A ::= v=v | v + K ≤ v
K ::= ... -2 | -1 | 0 | 1 | 2 | ...
v ::= x | y | z | ...  

Verify whether this language admits quantifier elimination.

• If it does admit quantifier-elimination, prove that this is the case by describing this algorithm informally, but precisely. The algorithm should take a formula of the form Qx.F where Q is a quantifier and F is quantifier-free, and it should eliminate the quantifier.
• If it does not admit quantifier elimination, give an example formula that you believe does not have a corresponding equivalent quantifier-free formula and describe constructs that you need to add to make quantifier elimination possible.

The basic ideas described in the class for dense linear orders should suffice to do this problem, but you need to change and adapt them to make them work for the ordering on integers. You can read the following papers to help you construct the proof, but cannot just say that the result follows from e.g. quantifier elimination of Presburger arithmetic. Indeed, the question is whether quantifier elimination is possible in this simpler language and not in the language of general Presburger arithmetic.

• On the theory of structural subtyping (especially Sections 3.1 and 3.2)
• Early technical report on BAPA (see only Appendix 11.1)
• JAR paper on BAPA

For in depth understanding you can also read references in there, in particular the relevant Wilfrid Hodges model theory book sections.

Hint: You should be able to reduce the problem to reasoning about conjunctions and generate a disjunction over total orders over terms of form v+c. Alternatively, you may be able to use some ideas of Fourier-Motzkin elimination, but it is not necessary for this problem to have an efficient algorithm, only an algorithm that works in principle.

1. Implement a verification condition generator that takes abstract syntax trees of the following form

S ::= (v=T)
    | assume(F)
    | assert(F)
    | havoc(v,...,v)
    | S ; S
    | while [inv F] (F) { S } 
    | if (F) { S } else { S }
T ::= T+T | T-T | K*T | v | K
A ::= T=T | T < T | True | False
F ::= A | (F&F) | (F|F) | ~F | ALL v.F | EX v.F
K ::= 0 | 1 | 2 | ...
v ::= x | y | z | ...

and computes a formula wp(S,F) for a given statement S and a given formula F. Here, the ASCII notation is the following:

& denotes conjunction
| denotes disjunction
ALL denotes universal quantifier
EX denotes existential quantifier

This notation corresponds to a fragment of the language of the Isabelle theorem prover, as well as the Jahob system.

The notation for while loop indicates that all loops have supplied loop invariants.

You do not need to build a parser for programs and formulas for this exercise, but it may make the testing of your implementation easier.

To make sure that you correctly avoid accidental variable capture, one of the many tests for your program should be the following 4 line sequence of commands:

x = 0;
y = x + 3;
havoc(x);
assert (y=3);

2. Given a statement S, compute wp(S,true) using the part 1, and pretty print it as a string conforming to the above grammar. Test your program on

• two input programs that generate valid formulas
• two input programs that generate invalid formulas

Try using the Isabelle theorem prover or formDecider in the Jahob system to prove the validity of the printed formulas and describe your experience.