Task 1
The property
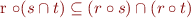
holds. Namely, suppose 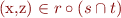 .
Then there is a y such
that
.
Then there is a y such
that 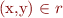 and
and  . Therefore,
. Therefore,
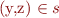 and
and 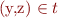 . From
. From 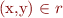 and
and 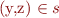 we
have
we
have  . Similarly,
from
. Similarly,
from 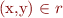 and
and 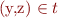 we
have
we
have  . Therefore,
. Therefore,  .
.
Task 2
The property
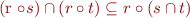
does not hold. As an example, take A={1,2}, B={p,q} and let
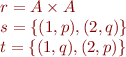
Task 3
(Sketch). By definitions of composition and inverse, both sides reduce to

Task 4
One way to prove it is to note that in the condition {P}r{Q}
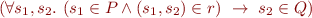
we can move quantification over s_2 inside and use properties of conjunction and implication to state it as:
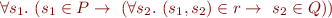
which is then equivalent to
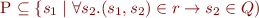
Therefore, the preconditions are precisely all subsets of the set on the right hand side, and so this set is the largest of them.
Alternatively, we can prove this property by showing by definition that 1) wp is a precondition and 2) that if we take any other precondition, it will be a subset of wp.
Task 5
The property
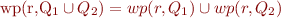
does not hold in general. As a counterexample, take three distinct states s_1, s_2, and s_3, and let
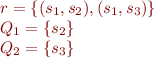
Note: the property does hold for deterministic relations.
Task 6
The property
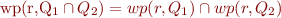
is true and follows from the characterization of wp in Task 4 and the distribution of the right-hand side of implication and universal quantification with respect to conjunction.