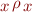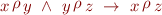This is an old revision of the document!
Preorder
A (reflexive) preorder relation  on set
on set  is a binary relation
is a binary relation 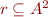 that is reflexive and transitive, that is, these two properties hold:
that is reflexive and transitive, that is, these two properties hold:
Constructing partial order from a preorder
Let  be a preorder. Define relation
be a preorder. Define relation  by
by
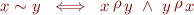
It is easy to verify that  is an equivalence relation. Moreover, if we define relation
is an equivalence relation. Moreover, if we define relation  on equivalence classes by
on equivalence classes by
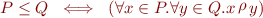
for  , then we can prove that
, then we can prove that  is a partial order.
is a partial order.