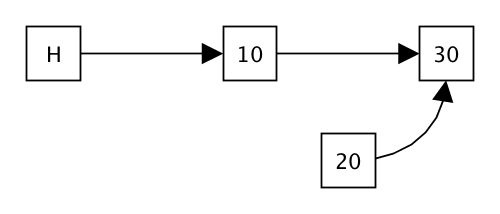
Lock-free Sorted List
See the page Setting up Assignment 6 for configuring your repository for this assignment.
Assignment Handout last updated: April 13, 17:35
The goal of this assignment is to implement a concurrent list that stores values of type Int in ascending order. Last week, we have seen how to use a monitor to make data structures operations behave correctly in a concurrent setting. This week, the data structure we will implement will not use a monitor or a lock of any kind. Instead, we will use an atomic operation, called compareAndSet, in your implementation of the data structure operations.
The goal will still be to have a data structure that can safely be used in a concurrent setting. In addition, the sorted list operations you will implement will be lock-free. In a system where all concurrent operations have this property, the progress of at least one thread is guaranteed. There can not be a global deadlock in which none of the threads can make progress! Note that this does not guarantee that all threads can make progress. An operation with this property is said to be wait-free.
Atomic Variables
The list methods you will implement will make use of atomic variables. An atomic variable is an object which holds a value of a given type T. The object offers two methods to manipulate this value: - get, which returns the current value held in the variable, - compareAndSet, which modifies the content of the variable provided that the previous value is given. This method returns true if it was successful, false otherwise.
The operation compareAndSet applies the following logic atomically, which means that there cannot be any context switches between the instructions of the operation:
def compareAndSet(expected: T, value: T) {
if (current == expected) {
current = value
true
}
else {
false
}
}
The AtomicVariable class is given to you. You do not have to worry about implementing it!
Note that a similar class exists in the Java standard library, called ''AtomicReference''. The main difference between AtomicReference and the AtomicVariable class we defined for this exercise is that AtomicReference uses referencial equality to check whether expected and current are the same, while AtomicVariable uses the == method.
The Sorted List Data Structure
The data structure you will implement is a mutable linked list of integers, sorted in ascending order. Each integer is stored in a Node. In addition to the integer value, each node contains a mutable reference to the next node in the list. This mutable reference is held in an AtomicVariable.
abstract class Node(val value: Int, initTail: Option[Node]) {
type State = Option[Node]
def initialState: State = initTail
val atomicState: AbstractAtomicVariable[State] = new AtomicVariable[State](initialState)
def next: Option[Node] = atomicState.get
// ...
}
Then, SortedList is simply a class which holds a reference to the first node of the list. This class is defined in SortedList.scala.
class SortedList extends AbstractSortedList {
// The sentinel node at the head.
private val _head = createNode(0, None, isHead=true)
// The first logical node is referenced by the head.
def firstNode: Option[Node] = _head.next
def findNodeWithPrev(pred: Int => Boolean): (Node, Option[Node]) = ???
def insert(e: Int): Unit = ???
def contains(e: Int): Boolean = ???
def delete(e: Int): Boolean = ???
}
The value _head of the list is called a sentinel node. This value (of type Node) will serve only as a reference to the first actual node of the list. The value (viz. zero) held by this special node should be completely ignored. This technique is useful because it limits the duplication of code. An alternative is to have a reference to the first node using an AtomicVariable. But this would force us to handle the first node differently from the rest. So will use a sentinel node for this assignment.
findNodeWithPrev
The first method you will implement is an internal helper method which will be used all other methods. This method should do a traversal of the list to find the first node whose value satisfies the parameter predicate. The method should return the following two values as a pair: - the predecessor of the node, - the node.
If node is the first node whose value satisfy the predicate and predecessor its predecessor, then the method should return (predecessor, Some(node)). Due to the use of the sentinel node at the head of the list, the method is bound to find a predecessor, even for the first logical node.
When the predicate doesn't hold on any of the values, then the function should return (last, None), where last is the last node of the list.
insert
Your first goal will be to code the insert method of the lock-free list. The idea is very simple:
- Locate the position you need to insert by using the
findNodeWithPrevmethod you have just implemented. - Create a new node which holds the value and points to the correct next node. For this, you should use
createNode(value, nextNode). - Use the
compareAndSetoperation to make the previous node point to your newly created node. - If the operation failed, retry from the start! Otherwise, the operation is done!
contains
Next, you should implement the contains method, which checks if the list contains a given element. You may of course use the findNodeWithPrev method you have implemented.
delete
With the addition of delete, things get rapidly trickier. The intuive solution would be to:
- Find the node to delete and its predecessor using
findNodeWithPrev. - Use an atomic
compareAndSetoperation to make the predecessor node point to the successor.
Unfortunately, this solution is not entirely satisfactory! Indeed, there exists schedules in which some successful operations are lost. Can you think of any?
As an example, assume that the list currently contains the values 10 and 30. 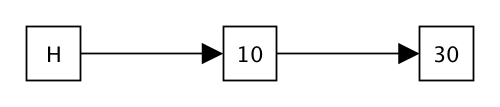
- Now, some other thread is scheduled and starts executing the deletion of the node with value
10. The thread find the two nodes that surrounds it, that is the sentinel node at the head of the list and the node with value30(note that the insertion of20by the other thread isn't visible yet!). The thread, using compare and set, changes the next pointer of the sentinel node to the node with value30. Thedeleteoperation then terminates successfully.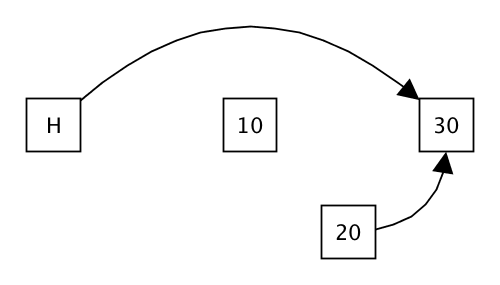
- Now, the first thread resumes its execution. Its next instruction is to use compare and set to change the next pointer of the node with value
10, which it can do without any problem! Indeed, this atomic variable wasn't touched by the delete operation. Theinsertoperation looks successful, eventhough the node that was inserted is not reachable from the head of the list! The operation was lost…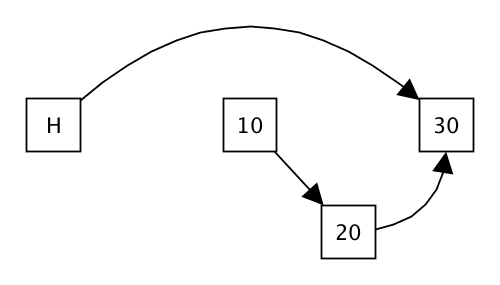
One solution to this problem, as proposed by Timothy L. Harris in his paper A Pragmatic Implementation of Non-Blocking Linked Lists, is to somehow record in the node that it was deleted. We will proceed in a similar fashion in this assignment.
Marking Nodes
The first step is to modify the mutable state held by nodes. Open the Node.scala file. Until now the state was just Option[Node], which is an optional reference to the next node. You will need to add, in addition to this information, a boolean flag that indicates whether the node was deleted or not.
abstract class Node(val value: Int, initTail: Option[Node]) {
type State = ???
def initialState: State = ???
val atomicState: AbstractAtomicVariable[State] = new AtomicVariable[State](initialState)
def next: Option[Node] = ???
def deleted: Boolean = ???
def mark: Boolean = ???
}
Begin by modifying the State type to any type that you deem appropriate. Remember that value of this type should contain an Option[Node] (the next node) and a flag (whether the node has been marked).
Complete the other functions, described below, as well: - initialState should return the state of the node when it is first created. Note that the node should not be marked and the optional reference to the next node should be set to initTail. - next should return the optional reference to the next node held currently in the state. - deleted should return true if the node was marked, false otherwise. - mark should mark the node as deleted. The method should return true only if it is the first time this node is marked. If the node was previously marked, this method should return false. (Think carefully about this!)
Implementing delete of SortedList
Now, we can implement a version of delete that is not vulnerable to the problem exposed earlier. The idea is to:
- Find the node to delete and its predecessor using
findNodeWithPrev. - Mark the node as
deletedusing itsmethod. If it returns false, retry from the start!
Once this is done, we still have to modify the other list methods to handle the fact that nodes can be marked.
Marked node will be deleted within the findNodeWithPrev method.
Adapting findNodeWithPrev to handle marked nodes
The first method you need to adapt is findNodeWithPrev. The method should do exactly as before except when it encounters a marked node during its traversal. When it does so, the method should use compareAndSet to modify the next node pointed by the predecessor node. Regardless of the outcome of the compareAndSet operation, the findNodeWithPrev should then restart from the head.
Adapting insert to handle marked nodes
The last method you need to change is insert. The logic remains exactly the same, except that when you perform the compareAndSet operation, you should make sure that the parameters are of type State and are not flagged as deleted.
You are now done with this assignment. Congratulations! You may test your solution using sbt test as usual. Once you are satisfied with your solution, do not forget to submit it and test it on the server. Use the deliverable tab to deliver the final version you want to be graded.