Expressing regular expressions in MSOL over strings

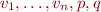Idea: for each regular expression $r$ of a automaton for parallel inputs $v_1,\ldots,v_n$ associate a formula $F$ with free variables $v_1,\ldots,v_n,p,q$ such that $F$ is valid precisely for whose sets of numbers for which

$p$ and $q$ are singletons
the strings given by the parts of $v_1,\ldots,v_n$ that start at position $p$ and end at position $q$ satisfy regular expression $F(r)$

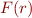
that the string (finite set from $p$ to $q$

... ap1 ... aq1 ...
... ap2 ... aq2 ...
... ...     ... ...
... apn ... aqn ...

The construction is by induction on the structure of regular expressions and resembles the description of parsing the string given by a regular expression:

base cases are easy
union is disjunction
concatenation existentially quantifies over middle position
iteration in 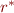$r^*$ quantifies over a set of positions between $p$ and $q$ at which a string can be broken into strings that satisfy $r$