Bitwidth Analysis
Given a language with signed 64 bit integers, determine as small as possible set of bits needed to store values of variables.
- e.g. if analysis derives that a subset of
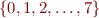 is sufficient, then we can use byte type to store the value
is sufficient, then we can use byte type to store the value- instead of having multiple integer types, we can have analysis infer the right 'subtypes' (ranges)
- the analysis becomes even more important if we generate hardware from C code: analysis would enable us to save circuits and power
Let B = {-32,-31,…,-1,0,1,…,31} be a set of bits.
Simple abstract domain (at each program point), map 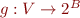 , specifying for each variable
, specifying for each variable  a subset of useful bits.
a subset of useful bits.
Abstract strongest postcondition for statement:
x = y + z
Updates possible bitwidth of  given bitwidths of
given bitwidths of  and
and 
One simple rule: 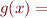
![Equation \begin{equation*}\begin{array}{l}
let\ L = \min(g(y)) + \min(g(z))-1 \\
let\ U = \max(g(y)) + \max(g(z))+1 \\
if\ (L < 32) \lor (U > 31)\ then\ B \\
else\ [L,U]
\end{array}
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img360642d2ed439e0554994154d9277acf.png)