Recursive Descent (Predictive) Parsing
Recursive descent is a decent parsing technique.
| descent: |
|---|
| a movement downward |
| decent: |
|---|
| adequate: sufficient for the purpose; “an adequate income”; “the food was adequate”; “a decent wage”; “enough food”; “good enough” |
(from Wordnet)
Basic Idea
- construct parse tree top-down
- use current symbol to decide which production to use
- write one procedure for constructing each non-terminal
- recursive non-terminals lead to recursive procedures
- alternative in grammar becomes 'if'
- repetition becomes 'while'
Example: Recursive Descent Parsing of Polynomials
In context-free grammars we have seen a grammar of polynomials.
Consider first this version of grammar:
- this grammar version is very nice for recursive descent parsing
Here is a parser for this grammar: polynomials.pscala
Note correspondence:
| (“+” term)* | ⇒ while (lex.current=PLUS) { lex.next; parseTerm } |
Example: running the code above on “x + y*(u+3)”
For statements, we use keyword to decide what we are about to parse:
| “if” X | “while” Y | ⇒ if (lex.current=IF) parseX else if (lex.current=WHILE) parseY |
Transforming Grammar: Left Factoring
Consider a variant of grammar with this definition:
polynomial ::= term | term "+" polynomial
How to write parsePolynomial procedure for this grammar?
- 'term' can be arbitrarily complex
- which alternative to choose?
Solution: apply left-factoring:
polynomial ::= term ("" | "+" polynomial)
Now we can construct parser:
def parsePolynomial = {
parseTerm
if (lex.current==PLUS) {
lex.next
parsePolynomial
}
}
We obtained tail-recursive version equivalent to a while loop.
Transforming Grammar: Left Recursion Makes Trouble
Instead of
polynomial ::= term ("" | "+" polynomial)
consider grammar defining the same language:
polynomial ::= ("" | polynomial "+") term
we need to parse polynomial, so we check which alternative to parse, so we check whether the current symbol is parsed by polynomial, so
we need to parse polynomial, so we check which alternative to parse, so we check whether the current symbol is parsed by polynomial, so
we need to parse polynomial, so we check which alternative to parse, so we check whether the current symbol is parsed by polynomial, so …
This does not work, because it contains left-recursive alternative
polynomial ::= polynomial "+" term
For recursive descent parsing, we need right-recursive rules, which work, like
polynomial ::= term "+" polynomial
Simple forms of right recursion can be expressed using repetition (and become while loops), which work.
Recursive Descent Parser for While Language
If you understand how we do this, you should be able to do it for MiniJava in homework as well.
The parser: WhileParser.scala
- simplified version of Concrete Syntax of While
- can connect to Hand-Written Scanner for While Language i.e. Lexer.scala
When Exactly Does Recursive Descent Work?
When can we be sure that recursive descent parser will parse grammar correctly?
- it will accept without error exactly when string can be derived
Consider grammar without repetition construct * (eliminate it using right recursion).
Given rules
X ::= p X ::= q
where p,q are sequences of terminals and non-terminals, we need to decide which one to use when parsing X, based on the first character of possible string given by p and q.
- first(p) - first characters of strings that p can generate
- first(q) - first characters of strings that q can generate
- requirement: first(p) and first(q) are disjoint
How to choose alternative: check whether current token belongs to first(p) or first(q)
Computing 'first' in Simple Case
Assume for now
- no non-terminal derives empty string, that is:
For every terminal X, if X =⇒* w and w is a string of terminals, then w is non-empty
We then have
- first(X …) = first(X)
- first(“a” …) = {a}
We compute first(p) set of terminals for
- every right-hand side alternative p, and
- every non-terminal X
Example grammar:
S ::= X | Y X ::= "b" | S Y Y ::= "a" X "b" | Y "b"
Equations:
- first(S) = first(X|Y) = first(X)
 first(Y)
first(Y) - first(X) = first(“b” | S Y) = first(“b”)
 first(S Y) = {b}
first(S Y) = {b}  first(S)
first(S)
How to solve equations for first?
Expansion: first(S) = first(X)  first(Y) = {b}
first(Y) = {b}  first(S)
first(S)  {a}
{a}  first(Y)
first(Y)
- could keep expanding forever
- does further expansion make difference?
- is there a solution?
- is there unique solution?
Bottom up computation, while there is change:
- initially all sets are empty
- if right hand side is bigger, add different to left-hand side
Solving equations
- first(S) = first(X)
 first(Y)
first(Y) - first(X) = {b}
 first(S)
first(S) - first(Y) = {a}
 first(Y)
first(Y)
bottom up
| first(S) | first(X) | first(Y) |
|---|---|---|
| {} | {} | {} |
| {} | {b} | {a} |
| {a,b} | {b} | {a} |
| {a,b} | {a,b} | {a} |
| {a,b} | {a,b} | {a} |
Does this process terminate?
- all sets are increasing
- a finite number of symbols in grammar
There is a unique least solution
- this is what we want to compute
- the above bottom up algorithm computes it
General Remark:
- this is an example of a 'fixed point' computation algorithm
- also be useful for semantic analysis, later
General Case: Nullable Non-terminals
In general, a non-terminal can expand to empty string
- example: statement sequence in while language grammar
A sequence of non-terminals is nullable if it can derive an empty string
- this is case iff each non-terminal is nullable
Computing nullable non-terminals:
- empty string is nullable
- if one right-hand side of non-terminal is nullable, so is the non-terminal
Algorithm:
nullable = {}
changed = true
while (changed) {
if X is not nullable and either
1) grammar contains rule
X ::= "" | ...
or
2) grammar contains rule
X ::= Y1 ... Yn | ...
and
{Y1,...,Yn} is contained in nullable
then
nullable = nullable union {X}
changed = true
}
Computing First Given Nullable
Computing first(X), given rule X = 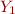 …
… 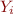 …
… 
- if
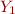 ,…,
,…, are all nullable, then add first(
are all nullable, then add first(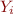 ) to first(X)
) to first(X)
Then repeat until no change, as before.
The Need for Follow
What if we have
X = Y Z | U
and U is nullable? When can we choose a nullable alternative (U)?
- if current token is either in first(U) or it could follow non-terminal X
t is in follow(X), if there exists a derivation containing substring X t
Example of language with 'named blocks':
statements ::= "" | statement statements statement ::= assign | block assign ::= ID "=" (ID|INT) ";" block ::= "begin" ID statements ID "end"
Try to parse
begin myPrettyCode x = 3; y = x; myPrettyCode end
Problem parsing 'statements':
- identifier could start alternative 'statement statements'
- identifier could follow 'statements', so we may wish to parse “”
Computing follow(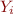 ), given rule X =
), given rule X = 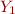 …
… 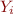 …
…  …
… 
- add first(
 ), if
), if  ,…,
,…, are all nullable
are all nullable - add follow(
 ), if
), if  , …,
, …,  are all nullable
are all nullable
Possible computation order:
- nullable
- first
- follow
Example: compute these values for grammar above
The grammar cannot be parsed because we have
statements ::= "" | statement statements
where
- statements
 nullable
nullable - first(statements)
 follow(statements) = {ID}
follow(statements) = {ID} 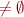
If the parser sees ID, it does not know if it should
- finish parsing 'statements' or
- parse another 'statement'
Recursive Descent Parsing
First, compute nullable, first, follow
Then, make parsing table which stores the alternative, given
- non-terminal being parsed (in which procedure we are)
- current token
Given (X ::= 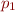 | … |
| … |  ) we insert alternative j into table iff
) we insert alternative j into table iff
- t
 first(p_j), or
first(p_j), or - nullable(
 ) and t
) and t  follow(X)
follow(X)
If in parsing table we have two or more alternatives for same token and non-terminal:
- we have conflict
- we cannot parse grammar using recursive descent
Otherwise, we say that the grammar is LL(1)
- left-to-right parse (the way input is examined)
- leftmost derivation (expand leftmost non-terminal first–recursion in descent does this)
- one token lookahead (current token)
What about empty entries?
- they indicate errors
- report that we expect one of tokens in
- first(X), if X
 nullable
nullable - first(X)
 follow(X), if X
follow(X), if X  nullable
nullable
Error Recovery
According to some opinions error recover is not worth it
- one error tends to trigger others
- report error and stop
- put cursor on the error
- restart when user fixes it
Approaches to error recovery in recursive descent parsing:
- insert some tokens (hard to guarantee termination)
- skip some tokens: when parsing X, skip until follow(X) or EOF
Summary
Recursive descent is decent because
- it is efficient
- it is simple enough to write by hand
- when we write by hand, we are not limited to following only grammar rules
- if e.g. multiple alternative begin with same ID, we can lookup previous declaration of ID and decide which alternative to follow
Exercise
Compute parsing table for WhileParser.scala.