Initialization Analysis
We follow the methodology of Designing Correct Data-Flow Analyses
Defining Properties of Interest
We represent program execution as a sequence of states  and simple statements
and simple statements  , starting with the initial state
, starting with the initial state
Given a sequence
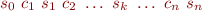
we say that variable  is initialized at step
is initialized at step  if one of the statements
if one of the statements 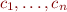 is an assignment to
is an assignment to  .
.
We say that a variable  is definitely initialized at program point
is definitely initialized at program point  , if for every execution that reaches program point
, if for every execution that reaches program point  , the variable
, the variable  is initialized at
is initialized at  .
.
We would like to compute the set of variables that are definitely initialized.
Reformulation of the Property
To avoid talking about previous states in a sequence and talk only about states, we use the following trick
- (an instance of a general technique of history variables)
For each variable, introduce an additional boolean flag (0 or 1) that indicates whether the variable is initialized
We have
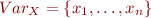 is the set of original variables
is the set of original variables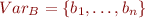 the corresponding boolean flags
the corresponding boolean flags
The state is map 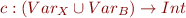
Then:
- at the beginning, all flags are 0
- at each assignment, we set the flag to 1
Desired property: if a statement reads a variable, then its flag must be 1
Defining Semilattice to Express Properties
We use
 to represent that the case when there are no states of initialization flag set to 0 (either there are no states at all, or there are only states with flag 1)
to represent that the case when there are no states of initialization flag set to 0 (either there are no states at all, or there are only states with flag 1)- in other words: initialized variable
 to represent states where initialization flag can be anything (0 or 1)
to represent states where initialization flag can be anything (0 or 1)- in other words: possibly uninitialized variable
Lattice element is map 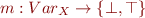
We use a pointwise lattice
Specifying Meaning of Lattice Elements
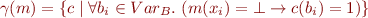
Example: Let 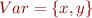 and let
and let 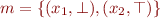 .
.
Then 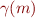 is the set of concrete states
is the set of concrete states  such that
such that 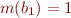 i.e.
i.e.  is initialized.
is initialized.
There is no constraint on  , because
, because 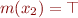 .
.
Checking monotonicity: if  then
then 
- note that if element in map goes from
 to
to  , then
, then  value gets only bigger
value gets only bigger
Initial Lattice Element
All points except entry get value  for each variable - as usual
for each variable - as usual
What can we assign to entry?
- all variables are uninitialized
- so all elements are

Transfer Functions
Two kinds of statements in CFG (ignoring procedure calls):
- dooes not change state (e.g. test) - initialization remains same
- they assign to some variable x - set initialization of x to
 (it is initialized)
(it is initialized)
Note on Procedures
What about procedure calls?
- for local variables - no change, procedure cannot change them
- for global variables
- who knows what procedure might do
- a safe thing is to set all global variables to

Intraprocedural analysis: analyzes one procedure at time
Interprocedural analysis: descend into procedures at call site
Using Results of Initialization Analysis
If at node  we have
we have 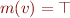 and there is a statement from
and there is a statement from  that reads
that reads  , report error
, report error