Designing Correct Data-Flow Analyses
Define Properties of Interest
Define precisely what property is needed (depends on the application), e.g.
- absence of errors
- potentially improving code performance without changing program meaning
Example: every variable assigned before being read
Define Analysis (Semi)Lattice to Express Properties
Find a lattice that
- encodes properties of interest
- enables terminating analysis
Specify lattice top, bottom, join
Precisely Specify Meaning of Lattice Elements
Specify concretization function, mapping lattice elements to sets of states
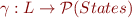
In SignAnalysis.scala, we have for 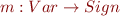 for
for 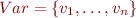
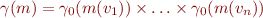
where, assuming infinite integers we have
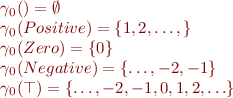
Monotonicity requirement for  :
:
 implies
implies  , for all
, for all 
Note that this implies
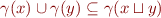
Example
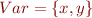
Lattice element 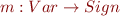 given by
given by 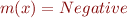 ,
, 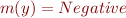
Then
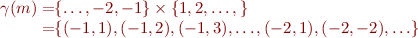
Here we wrote 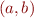 to mean the function
to mean the function 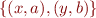 .
.
Compute a Sound Initial Lattice Element
Initially, the set of reachable states is empty at all points, except at CFG entry, where we have set of initial states of program 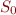
In the initial state of data-flow analysis, we will assign  to each program location except entry
to each program location except entry
At entry we assign lattice element  such that
such that
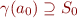
Derive Sound Transfer Functions
For each statement 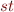 , define
, define 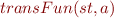
Needs to correctly approximate the effect of statement 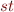 on states given by
on states given by  .
.
Formally, for all statements 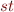 and lattice elements
and lattice elements  the correctness condition is:
the correctness condition is:
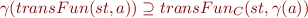
Here 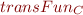 is the transfer function from Concrete Execution as Data-Flow Analysis
is the transfer function from Concrete Execution as Data-Flow Analysis
- takes set of states and runs statement
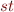 on each state
on each state
Recall SignAnalysis.scala transfer functions
Sketch of Correctness Proof
Why are computed results correct?
Imagine running in parallel a step of
- our data flow analysis (abstract analysis)
We can show, for each 
- at step
 results in abstract analysis approximate concrete execution of up to step
results in abstract analysis approximate concrete execution of up to step 
We can show that in the limit, this approximation holds
- limit of concrete data-flow analysis computes set of reachable states
- thus, the compute results approximate reachable states
This can be made completely precise using theory of lattices and fixed points