Homework 3
Due by Wednesday, 31st October, 10:15am sharp (right before the class).
Problem 1
We want to construct an LL(1) parser for the following grammar.
S -> ( L ) S -> a L -> L , S L -> S
a) Can the grammar be used with a LL(1) parser as is? If not, modify it accordingly.
b) Compute the First and Follow sets for S and L for the new grammar.
c) Finally, construct the parsing table.
Problem 2
A grammar has a cycle if there is a non-terminal  such that
such that 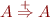 ,
i.e. it is possible to derive the nonterminal A from A by a nonempty sequence of production rules.
,
i.e. it is possible to derive the nonterminal A from A by a nonempty sequence of production rules.
a) Show that an LL(1) grammar is not allowed to have any cycles. Recall, that an LL(1) grammar is one for which a predictive parser needs just one look-ahead symbol.
b) Give an algorithm that eliminates cycles in a context-free grammar.
Problem 3
Show that the regular languages can be recognized with LL(1) parsers. Describe a process that, given a regular expression, constructs an LL(1) parser for it.
Problem 4
Put the following grammar into Chomsky normal form. Show your steps (i.e. don't just give the final grammar without explanation, or we won't be able/willing to check that it describes the same language).
S -> A ( S ) B | ε A -> S | S B | x | ε B -> S B | y
Problem 5
Assume a grammar in Chomsky normal form has  non-terminals. Show that if the grammar can generate a word with a derivation having at least
non-terminals. Show that if the grammar can generate a word with a derivation having at least  steps, then the recognized language should be infinite.
steps, then the recognized language should be infinite.