Partial Orders for Approximation
To solve complex constraints in numerical analysis, and in program analysis, we can use approximation techniques.
We use partial orders to describe approximation.
In numerical analysis the order is order on real numbers.
Example: if we are approximating some exact real value such as  from above, then
from above, then
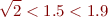
and we have that 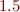 is than
is than 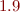 in approximating
in approximating  .
.
In program analysis states often have discrete structures, so our orders are more like subset relations.
Example: if the set of possible values of a variable at some program point is 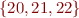 then we have
then we have
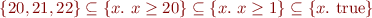
so among the three sets,  is the best approximation of
is the best approximation of 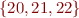 .
.
To avoid working with all possible sets of states, we work with some subset of the set of states. This subset will form a structure such as lattice.
Basic plan:
- represent semantics as limits of sequences in partial order elements (the Collecting Semantics)
- approximate the semantics of a lattice with a simpler abstract lattice (used to represent space of loop invariants)
- compute limits of sequences in the simpler abstract lattice
- prove that approximation is conservative, a computed invariant is a always a true property (in worst case it is 'true')