LARA

Lecture 06

lecture notes

Earley Parser

Continued in Lecture 07

Exercise 1

Given the following grammar: 

S → AaB | aBb
A → a | C
B → FAb |  bA
C → CDB | ϵ
D → A | B | ab
E → b | A
F → aF
  • Remove ϵ-productions, unit productions and useless non-terminals.
  • Put the resulting grammar into Chomsky Normal Form.
  • Argue if it is possible to apply the modifications in the first part in different orders.

Exercise 2

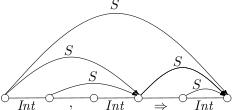
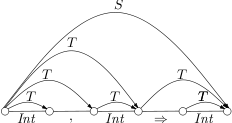
A CYK parser is parsing the input “Int , Int ⇒ Int”. The incomplete tables for two different grammars are given below.

  • Complete the table.
  • Find the suitable grammar that actually generates the table.
  • Construct the table for “Int , Int ⇒ Int , Int”.

a)

b)

Exercise 3

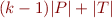Consider a context-free grammar without unit or ε-productions. Assume that the maximum number of symbols on the right hand side of any production is $k$. Show that there exists an equivalent grammar in Chomsky normal form with no more than $(k - 1)|P| + |T|$ production rules. The set $P$ is the set of production rules and $T$ is the set of terminals.