Register Allocation using Liveness Information
static int x; static int y; static int z; static int res; int f() { int xy; int yz; int xz; int res1; xy = x * y; yz = y * z; xz = x * z; res1 = xy + yz; res = res1 + xz; }
How to generate code that we saw in Register Machine Model in Scala
Move(Register(1), Memory(xAddr)),
Move(Register(2), Memory(yAddr)),
Move(Register(3), Memory(zAddr)),
Quad(Register(4), Mul, Register(1), Register(2)),
Quad(Register(2), Mul, Register(2), Register(3)),
Quad(Register(4), Add, Register(4), Register(2)),
Quad(Register(1), Mul, Register(1), Register(3)),
Quad(Register(4), Add, Register(4), Register(1)),
Move(Memory(rAddr), Register(4))
One solution:
- keep variables in registers when possible
- reuse registers if variable not used any more
- if no available register, free a register by saving it to memory ('spilling')
A lot of research was done and better techiques were found
Liveness in the Example
Variable is not live at a given program point if its current value will not be used in any future execution.
| code | live variables |
|---|---|
| {} | |
| x = xAddr | |
| {x} | |
| y = yAddr | |
| {x,y} | |
| xy = x * y | |
| {xy,x,y} | |
| z = zAddr | |
| {xy,x,y,z} | |
| yz = y * z | |
| {xy,yz,x,z} | |
| xz = x * z | |
| {xy, yz,xz} | |
| res1 = xy + yz | |
| {res1,xz} | |
| res = res1 + xz | |
| {} |
Slightly differently ordered program:
| code | live variables |
|---|---|
| {} | |
| x = xAddr | |
| {x} | |
| y = yAddr | |
| {x,y} | |
| xy = x * y | |
| {xy,x,y} | |
| z = zAddr | |
| {xy,x,y,z} | |
| yz = y * z | |
| {xy,yz,x,z} | |
| res1 = xy + yz | |
| {res1,x,z} | |
| xz = x * z | |
| {res1,xz} | |
| res = res1 + xz | |
| {} |
Interference Graph
Undirected graph
Nodes are variables: x,y,z,xy,yz,xz,res1
Edges: there is an edge 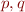 if at some program point
if at some program point  , we have
, we have 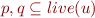
- both variables are live at the same time at some point
A Register Allocation Algorithm
Starting point:
- assign variables to memory
- assume temporary (intermediate) values will be in registers
- introduce explicit instructions to move between memory and registers
Goal is to assign temporaries to a limited number of K registers
If two temporary variables are both live at same point, we cannot keep them in same register
Algorithm phases:
Build: construct interference graph
- nodes are temporary variables
- there is edge if two variables both live at some program point
Goal: color the graph using K colors such that adjecent nodes have different color
- colors are registers
- if we need values of two temporaries, we can store them in different registers
Simplify
If there is a node with less than K neighbors, we will always be able to color it!
- so we can remove it from the graph
This reduces graph size
- it is incomplete
- e.g. every planar can be colored by at most 4 colors (and can have nodes with 100 neighbors)
Spill
If every node has K or more neighbors, we remove one of them
- we mark it as node for potential spilling
- then remove it and continue
Select
Assign colors backwards, adding nodes that were removed
If we find a node that was spilled, we check if we are lucky that we can color it
- if yes, continue
- if no, insert instructions to save and load values from memory
- restart (now we have graph that is easier to color)
For the first of the examples, we can remove the nodes e.g. in this order:
res1 xz xy y x z yz
This gives a 4-coloring
Suppose we try to do it with 3 registers only. We get potential spill trying to color xy. So we change the program to introduce a location in memory (e.g. on stack frame) to store the value of xy right after we assign to it and reload it immediately afterwards. We get this program:
| code | live variables |
|---|---|
| {} | |
| x = xAddr | |
| {x} | |
| y = yAddr | |
| {x,y} | |
| xy = x * y | |
| {x,y,xy} | |
| xyAddr = xy | |
| {x,y} | |
| z = zAddr | |
| {x,y,z} | |
| yz = y * z | |
| {yz,x,z} | |
| xz = x * z | |
| {yz,xz} | |
| xy1 = xyAddr | |
| {xy1,yz,xz} | |
| res1 = xy1 + yz | |
| {res1,xz} | |
| res = res1 + xz | |
| {} |
Note that xy was split into xy and xy1, each of which has shorter life span. It “hibernates” in memory and is woken up when the value is loaded.
We succeed in coloring it, e.g. with these colors:
res1 -> 1 xz -> 3 xy1 -> 2 yz -> 1 xy -> 1 y -> 3 x -> 2 z -> 1
Conservative Coalescing
Suppose that variables tmp1 and tmp2 are both assigned to the same register R and the program has an instruction:
tmp2 = tmp1
which moves the value of tmp1 into tmp2. This instruction then becomes
R = R
which can be simply omitted.
How to force a register allocator to assign tmp1 and tmp2 to same register?
- merge the nodes for tmp1 and tmp2 in the interference graph
- this is called coalescing
If we always coalesce non-interfering nodes when there are assignments, then our graph may become more difficult to color, and we may in fact need more registers!
Conservative coalescing: coalesce only if merged node of tmp1 and tmp2 will have a small degree so that we are sure that we will be able to color it.
Example 1
i = 0 s = s + i i = i + b j = i s = s + j + b j = j + 1
Live variables:
| code | live variables |
|---|---|
| {s,b} | |
| i = 0 | |
| {s,b,i} | |
| s = s + i | |
| {s,b,i} | |
| i = i + b | |
| {s,b,i} | |
| j = i | |
| {s,j,b} | |
| s = s + j +b | |
| {j} | |
| j = j + 1 | |
| {} |
Example 2
References
- Tiger book, Chapter 11