Limitations of Regular Expressions
Take a deterministic finite state machine  with
with  states.
states.
Suppose that a word of  with
with  is accepted by the machine. This means that the machine went through some state twice, say after reading
is accepted by the machine. This means that the machine went through some state twice, say after reading  and then after reading
and then after reading 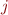 symbols of the word.
symbols of the word.
Then for some words 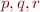 with
with 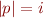 and
and 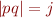 we have
we have  where the state after reading
where the state after reading  and state after reading
and state after reading  are the same. Then it means that the machine is in the same state after reading
are the same. Then it means that the machine is in the same state after reading 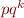 for any
for any 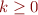 , so all words of the form
, so all words of the form 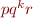 are accepted by the machine.
are accepted by the machine.
This is a rough statement of the so called “pumping lemma”.
Example of application: The language 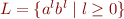 is not regular. Suppose the contrary. Then there is a machine
is not regular. Suppose the contrary. Then there is a machine  that accepts the language; let
that accepts the language; let  be the number of states of
be the number of states of  . The word
. The word 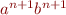 is accepted by
is accepted by  . While reading the prefix
. While reading the prefix  the machine must go through some state twice. If we skip this loop, then there is a word of the form
the machine must go through some state twice. If we skip this loop, then there is a word of the form 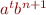 for
for 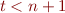 that is also accepted, which is contradiction with the condition that
that is also accepted, which is contradiction with the condition that  accepts
accepts  .
.