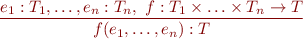Idea of Type Rules
Notation for Type Rules
We write 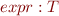 to indicate that
to indicate that
 is well-typed inside and has resulting type
is well-typed inside and has resulting type 
Examples:
Type rule for addition:
e1 : Int, e2 : Int
------------------
e1+e2 : Int
For <=:
e1 : int, e2 : int
------------------
e1<=e2 : boolean
Type derivation for
3 + 5 <= 9
is the following
3 : Int, 5 : Int
---------------- , 9 : Int
3 + 5 : Int
---------------------------
(3 + 5 <= 9) : boolean
Type Rule for Function Application
We have
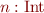




- for user-defined functions, rules are given by their declaration
The general rule for operation  is:
is:
- if
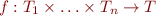 ,
, - and
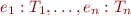 ,
, - then
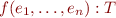
We write this as the following application typing rule: