LARA

Homework 04

To be handed out on October 21st, 2009, together with Homework 03.

Consider the following grammar of a simple programming language: 

S :::= E eof
E ::= if (E) E 
E ::= if (E) E else E
E ::= E + E
E ::= (E)
E ::= ID

where the tokens are: 

eof, if, (, ), else, +, id

and nonterminals are S, E.

Part a):

Compute the set follow(E).

Part b):

According to Automata for LR Parsing without Lookahead, draw an automaton whose states are sets of LR(0) items and edges are given by the corresponding goto function. Give a name to each state (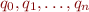$q_0, q_1, \ldots, q_n$).

Part c):

Consider the behavior of an SLR Parser for this grammar. List all states $q_i$ that have a conflict where multiple shift or reduce actions are possible. For each such state $q_i$:

  • show an example program that satisfies the grammar and causes the automaton to reach $q_i$ during parsing
  • is it possible to add parentheses (…) to the example so that the parser does not encounter the state $q_i$?
  • recommend a way of resolving the conflicts using associativity rules, if possible

Solution