Exercises 04
Exercise 1
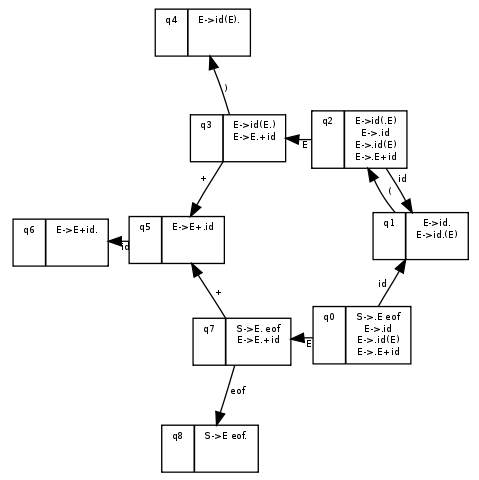
a) Build the LR(0) DFA for this grammar:
S → E eof E → id E → id (E) E → E + id
b) Is this an LR(0) grammar? Give evidence.
c) Is this an SLR grammar? Give evidence.
d) Is this an LR(1) grammar? Give evidence.
Solution:
b) This is not an LR(0) grammar: when parsing the string “id(”, in state q1 we can either reduce “E → id.” or we can shift “(” and go to q2.
c) An SLR parser uses follow sets, let's compute them:
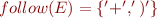
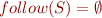
The conflict at node q1 is resolved because we can reduce “E → id.” only if 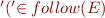 , which is not the case. We thus have only one choice, shift '(' and go to q2.
, which is not the case. We thus have only one choice, shift '(' and go to q2.
Example: run of the algorithm with input “id(id)” (the stack grows from left to right).
- Current token: “id”, Stack: q0 | only shift is possible (no rule ending with .): push id, q1 on the stack, go to q1.
- Current token: “(”, Stack: q0, “id”, q1 | only shift is possible, reduce rule “E → id.” is not possible because the current token (“(”) is not in follow(E): push “(”, q2 on the stack, go to q2.
- Current token: “id”, Stack: q0, “id”, q1, “(”, q2 | only shift is possible (no rule ending with .): push “id”, q1 on the stack, go to q1.
- Current token: “)”, Stack: q0, “id”, q1, “(”, q2, “id”, q1 | shift is not possible (the current token is “)”, but reducing rule “E → id.” is possible because “)” is in follow(E): pop “id”, q1 from the stack and push E, q3 (because from q2 the automaton goes to q3 on input E).
- Current token: “)”, Stack: q0, “id”, q1, “(”, q2, E, q3 | only shift is possible, push “)”, q4.
- Current token: “eof”, Stack: q0, “id”, q1, “(”, q2, E, q3, “)”, q4 | only reducing rule “E → id(E).” is possible: pop “id”, q1, “(”, q2, E, q3, “)”, q4 from the stack and push E, q7 (because from q0 we go to q7 on input E).
- Current token: “eof”, Stack: q0, E, q7 | only shift is possible: push “eof”, q8. FINISHED
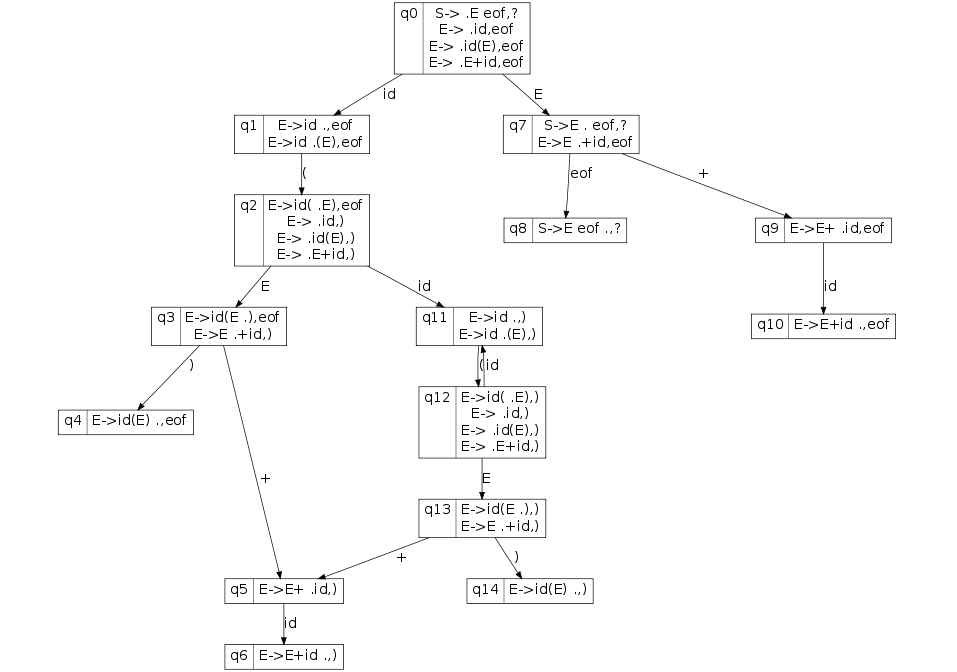
c) We said that the grammar is SLR, because all SLR grammars are LR(1), we can say the grammar is LR(1) too.
Example: LR(1) automaton, the algorithm run is similar to the previous one.
Exercise 2
Consider the following grammar:
S → E eof \\ E → while E do E\\ E → E ^ E\\ E → (E)\\ E → ID\\
a) Compute the set follow(E).
b) Build the automaton (draw it or give the states and transition table) for LR(0) parsing of this grammar (according to Automata for LR Parsing without Lookahead).
c) Consider the behavior of the LR(0) parser using the automaton. Are there any shift-reduce conflicts ?