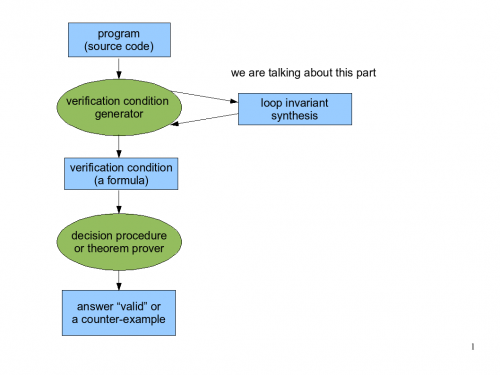
Lecture 9 Skeleton
Recall formula propagation from Lecture 7. See correctness of formula propagation.
Static analysis as equation solving in a lattice
If instead of formulas as 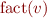 we have elements of some lattice, this condition becomes
we have elements of some lattice, this condition becomes
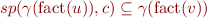
(where sp in now denotes operator on states and not formulas).
By properties of Galois connection, this is equivalent to
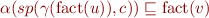
and we defined best transformer as 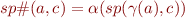 , so this condition is equivalent to
, so this condition is equivalent to
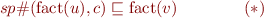
We conclude that finding an inductive invariant expressed using elements of a lattice corresponds to finding a solution to a system of inequations  for all
for all 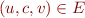 . We next examine the existence and computation of such solutions more generally.
. We next examine the existence and computation of such solutions more generally.
Note that 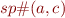 is a function monotonic in a. Why?
is a function monotonic in a. Why?
So, we are solving a conjunction of inequations
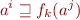
where  are variables ranging over a lattice
are variables ranging over a lattice  (one for each control-flow graph node), and
(one for each control-flow graph node), and  are monotonic functions on
are monotonic functions on  (one for each edge in the control-flow graph).
(one for each edge in the control-flow graph).
From a system of equations to one equation
In lattice, we have that a conjunction of inequations
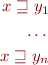
is equivalent to 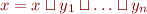 (
( is least upper bound of them).
is least upper bound of them).
So we can write the conjunction of inequations in the previous section as a system of equations
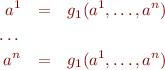
Now, introduce a new product lattice 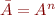 with order
with order
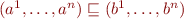 iff
iff 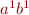 ,\ldots,
,\ldots,  all hold. Then we have reduced the problem to finding a solution to equation
all hold. Then we have reduced the problem to finding a solution to equation
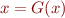
where  . Function
. Function  is also monotonic.
is also monotonic.
The solution of equation of the form 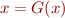 is called a fixed point of function
is called a fixed point of function  , because
, because  leaves
leaves  in place.
in place.
The iterative process that we described above corresponds to picking an initial element  such that
such that  and then computing
and then computing 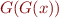 , \ldots,
, \ldots, 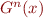 .
.
- we have

- we have

If it stabilizes we have 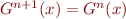 , so
, so 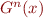 is a fixed point. This always happens if there are no infinite ascending chains.
is a fixed point. This always happens if there are no infinite ascending chains.
What is we have arbitrary lattices? See, for example non-converging iteration in reals.
 -continuity in a complete lattice is a requirement that for every chain
-continuity in a complete lattice is a requirement that for every chain  we have
we have
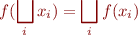
(generalizes continuity in real numbers). For continuous functions, even if there are infinite ascending chains, the fixed point iteration converges in the limit.
In general, even without  -continuity we know that the fixed point exists, due to Tarski fixed point theorem.
-continuity we know that the fixed point exists, due to Tarski fixed point theorem.
See also lecture notes in SAV07 resource page, in particular notes by Michael Schwartzbach for the finite case and slides by David Schmidt for  -continuity.
You can also check papers by Cousot & Cousot:
-continuity.
You can also check papers by Cousot & Cousot: